Como Sacar La Base De Un Triángulo Isósceles

Enseñar a los estudiantes a calcular la base de un triángulo isósceles puede ser un desafío. La clave reside en comprender sus propiedades y aplicar las herramientas adecuadas. Aquí exploraremos métodos y estrategias para facilitar este proceso.
Identificando las Propiedades Clave
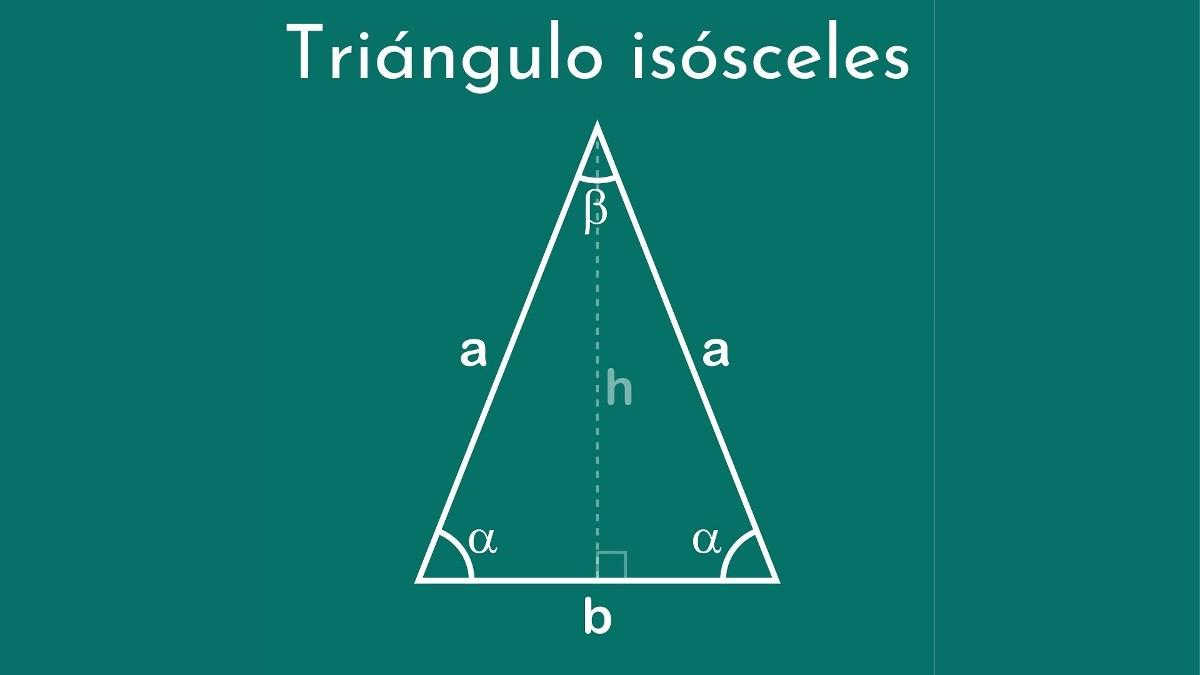
Un triángulo isósceles se caracteriza por tener dos lados iguales. Estos lados iguales también implican que los ángulos opuestos a ellos son iguales. Reconocer estas propiedades es el primer paso.
La altura trazada desde el vértice, donde se unen los dos lados iguales, biseca la base. Esta altura forma dos triángulos rectángulos congruentes. Esta división es crucial para aplicar el Teorema de Pitágoras.
Es fundamental recordar que la base es el lado diferente. Es el lado que no es igual a los otros dos lados congruentes. Ayuda a los estudiantes a visualizar esta diferencia claramente.
Usando el Teorema de Pitágoras
Si conoces la longitud de uno de los lados iguales y la altura, puedes aplicar el Teorema de Pitágoras. Primero, considera uno de los triángulos rectángulos formados por la altura. La altura es uno de los catetos.
El lado igual del triángulo isósceles es la hipotenusa. La mitad de la base es el otro cateto. Así, podemos plantear la ecuación: (lado igual)² = (altura)² + (mitad de la base)².
Despeja (mitad de la base)². Luego, calcula la raíz cuadrada para obtener la mitad de la longitud de la base. Finalmente, multiplica este valor por dos para obtener la longitud total de la base. Practica con varios ejemplos para consolidar la comprensión.
Conociendo el Área y la Altura
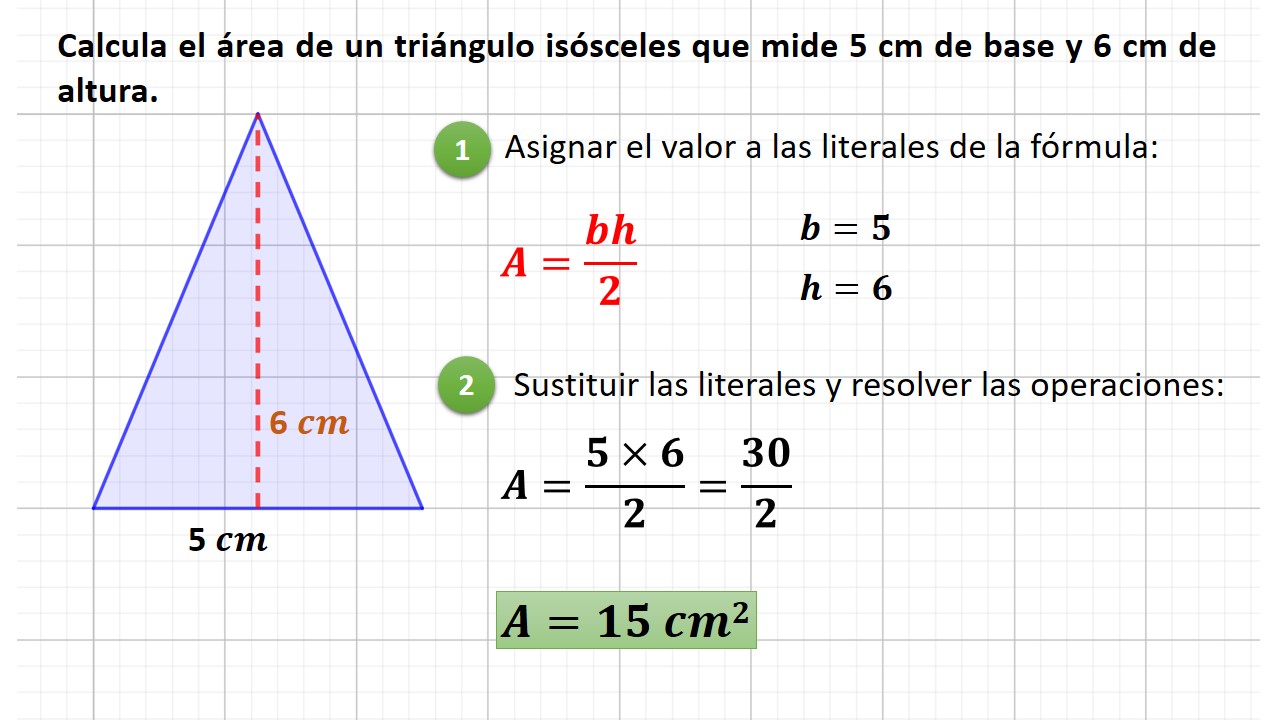
Si conoces el área del triángulo isósceles y su altura, puedes usar la fórmula del área. Recuerda que el área de un triángulo es: Área = (base * altura) / 2. Este método es útil si la longitud de los lados iguales no está disponible.
Despeja la base de la fórmula: base = (2 * Área) / altura. Introduce los valores conocidos del área y la altura. Realiza la operación para obtener la longitud de la base.
Este método resalta la relación entre el área, la base y la altura. Es una excelente forma de reforzar conceptos previos sobre áreas de triángulos.
Estrategias para la Enseñanza
Utiliza representaciones visuales. Diagramas claros y bien etiquetados son esenciales. Ayudan a los estudiantes a visualizar las relaciones entre los lados, la altura y la base.
Comienza con ejemplos sencillos. Aumenta gradualmente la complejidad de los problemas. Asegúrate de que comprendan los fundamentos antes de abordar problemas más desafiantes.
Fomenta la participación activa. Pídeles a los estudiantes que dibujen sus propios triángulos. Anímales a explicar sus razonamientos en voz alta. Esto ayuda a identificar y corregir errores conceptuales.
Errores Comunes
Confundir la hipotenusa con un cateto. Asegúrate de que comprendan qué lado es la hipotenusa en el triángulo rectángulo formado. Refuerza la identificación de la hipotenusa como el lado opuesto al ángulo recto.
Olvidar multiplicar por dos. Recuerda que el cálculo inicial da la mitad de la base. Asegúrate de que multipliquen ese valor por dos para obtener la longitud completa.
No identificar correctamente la altura. La altura debe ser perpendicular a la base. A veces los estudiantes confunden otros lados con la altura. Utiliza ejemplos donde la orientación del triángulo varía.
Haciendo el Aprendizaje Atractivo
Incorpora actividades prácticas. Utiliza reglas, compases y transportadores para construir triángulos isósceles. Mide sus lados y ángulos para verificar las propiedades.
Presenta problemas del mundo real. Por ejemplo, calcular la base de un techo con forma de triángulo isósceles. Estos problemas ayudan a conectar las matemáticas con situaciones cotidianas.
Usa juegos y desafíos. Crea concursos donde los estudiantes resuelvan problemas en equipos. Introduce elementos de gamificación para aumentar el interés y la motivación.