Cuales Son Las Funciones Cuadraticas Ejemplos

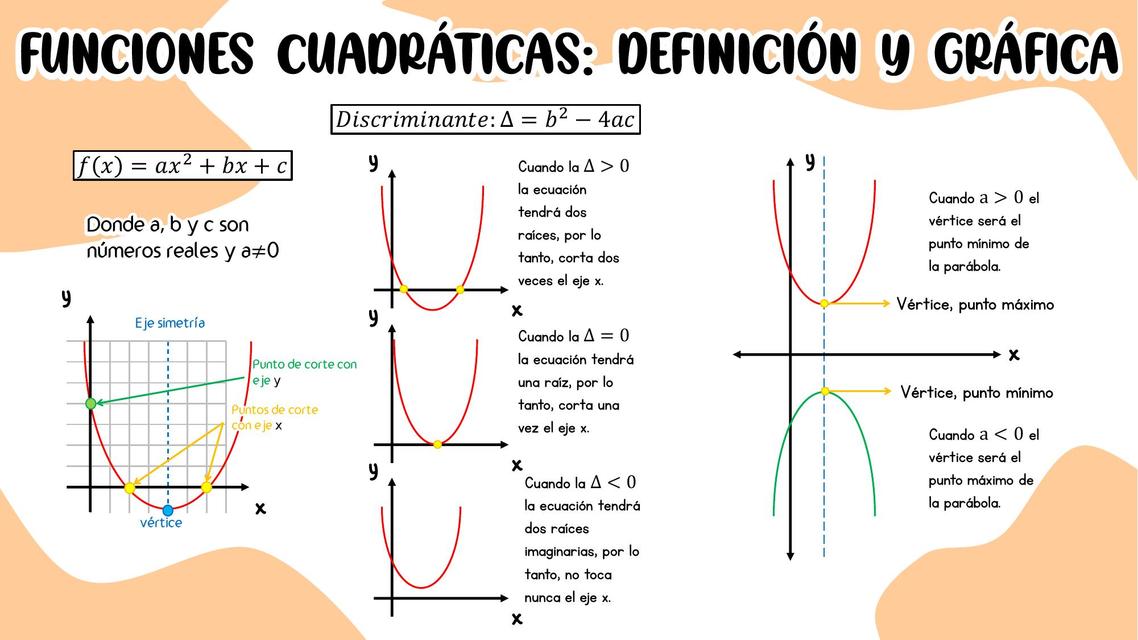
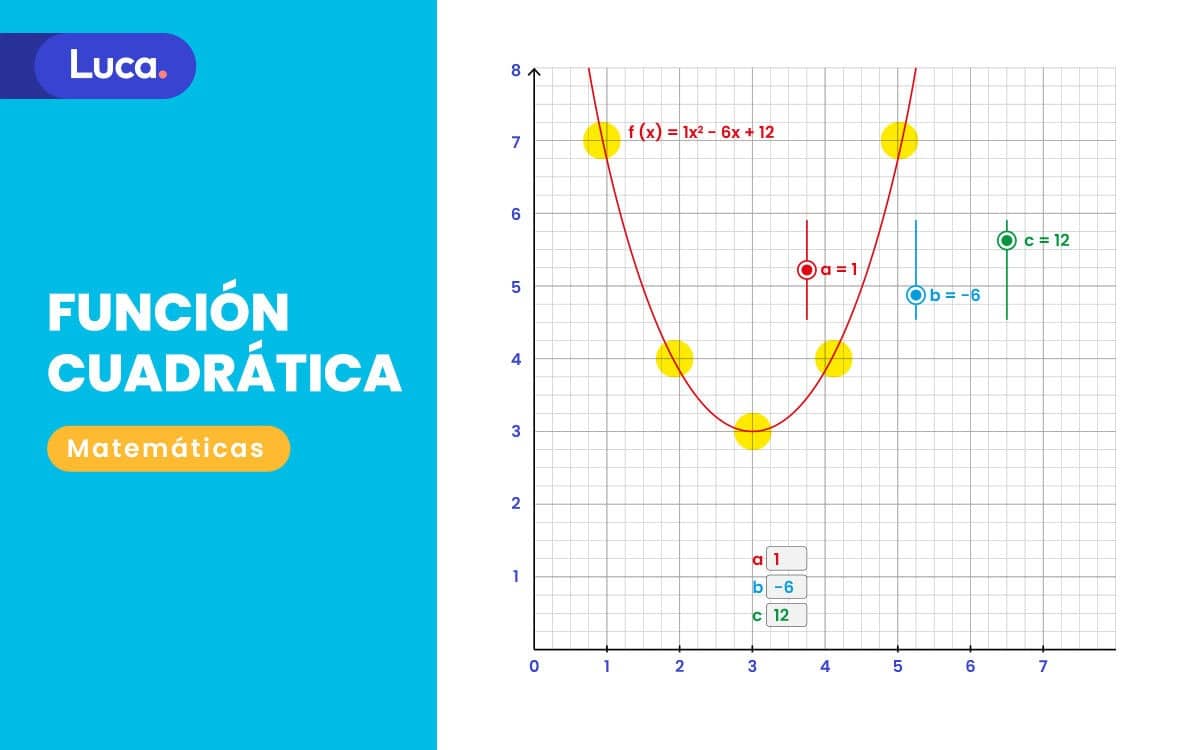
Una función cuadrática es una función polinómica de grado 2. Esto significa que la variable independiente (generalmente 'x') está elevada al cuadrado (x²) como máximo exponente. La forma general de una función cuadrática es: f(x) = ax² + bx + c, donde a, b y c son constantes, y lo más importante, a no puede ser cero.

Identificando los Componentes:

• a: Este coeficiente determina si la parábola se abre hacia arriba (a > 0) o hacia abajo (a < 0). También influye en la "amplitud" de la parábola; un valor absoluto mayor de 'a' hace que la parábola sea más estrecha.
• b: Este coeficiente afecta la posición del eje de simetría de la parábola.
• c: Este coeficiente representa el punto de intersección de la parábola con el eje y (cuando x = 0).

Ejemplos de Funciones Cuadráticas:

Ejemplo 1: f(x) = 2x² + 3x - 5

Aquí, a = 2, b = 3, y c = -5. La parábola se abre hacia arriba porque a > 0.

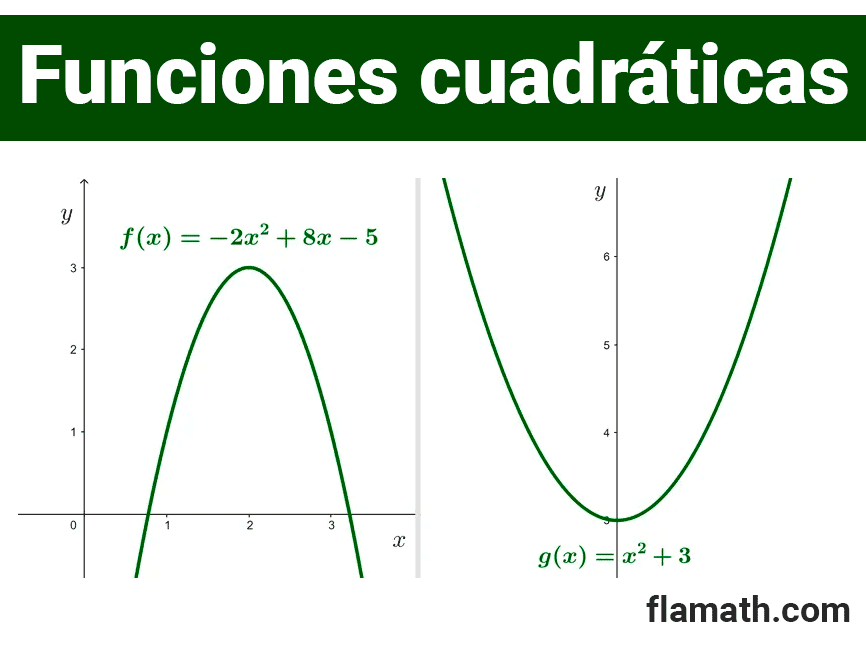
Ejemplo 2: g(x) = -x² + 4

Aquí, a = -1, b = 0, y c = 4. La parábola se abre hacia abajo porque a < 0, y su eje de simetría está en x = 0 (el eje y).

Ejemplo 3: h(x) = x²

Aquí, a = 1, b = 0, y c = 0. Esta es la función cuadrática más básica, con el vértice en el origen (0,0).

La Gráfica: la Parábola

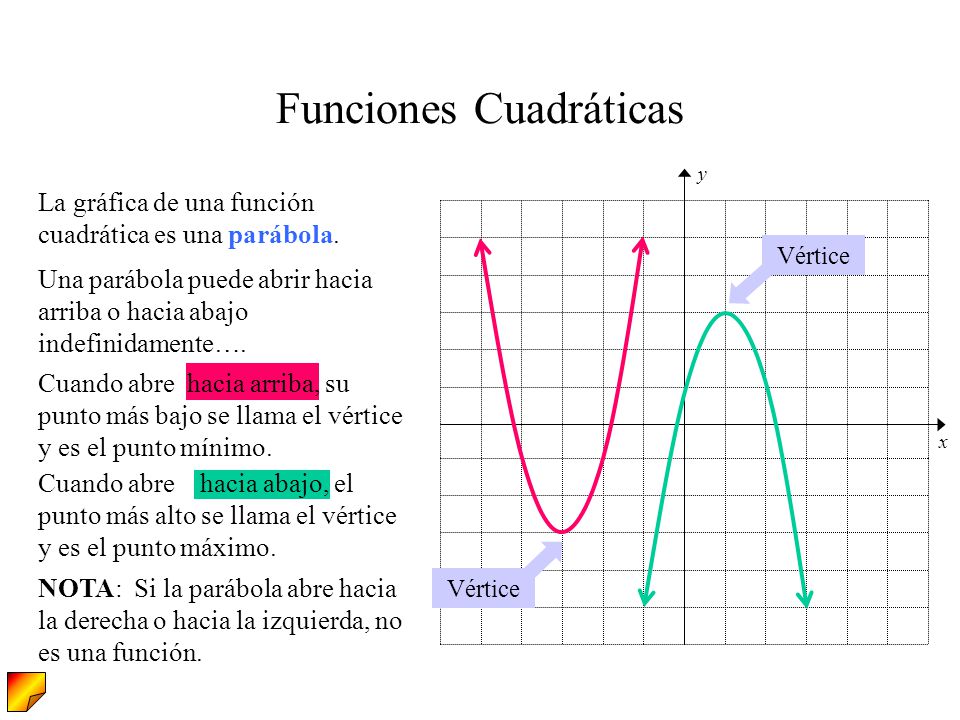
La gráfica de una función cuadrática es una curva llamada parábola. La parábola tiene un punto máximo o mínimo, llamado vértice. El vértice es importante para entender el comportamiento de la función. La línea vertical que pasa por el vértice es el eje de simetría; la parábola es simétrica con respecto a este eje.

Encontrar el Vértice:

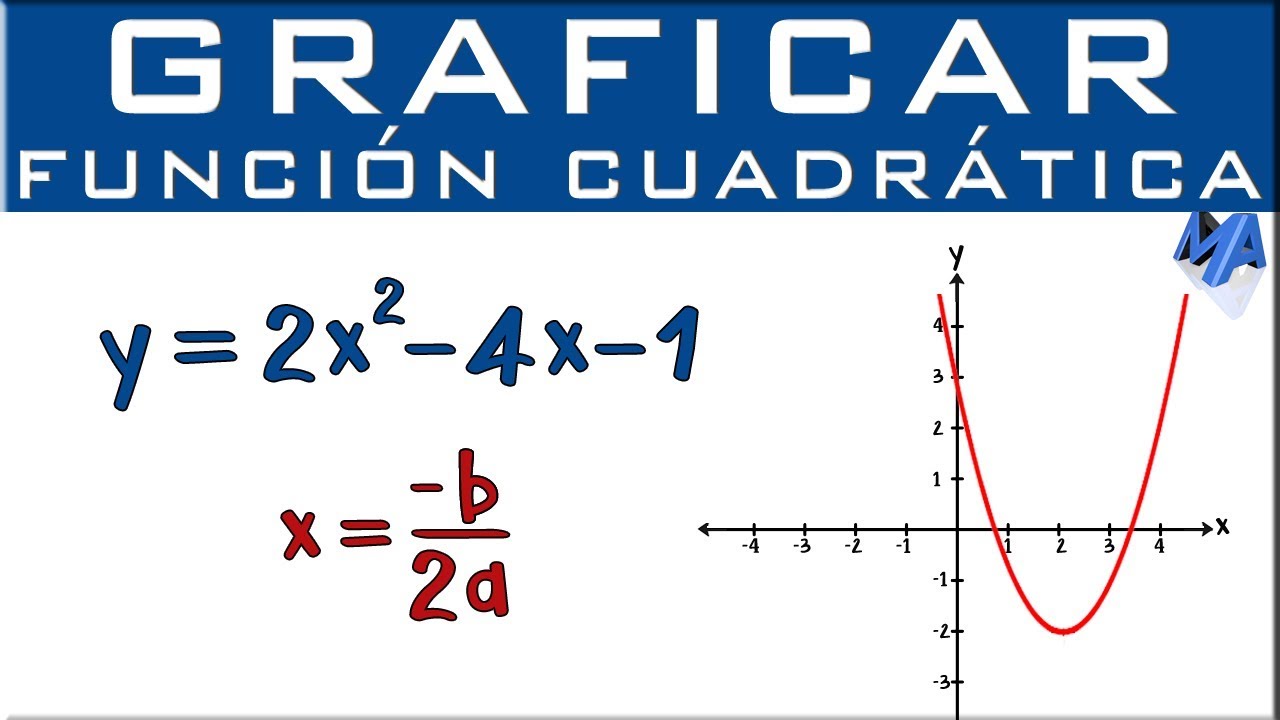
La coordenada x del vértice se puede encontrar con la fórmula: x = -b / 2a. Luego, se sustituye este valor de x en la función para encontrar la coordenada y del vértice.

En resumen, las funciones cuadráticas son una herramienta importante en matemáticas y se utilizan para modelar una variedad de fenómenos del mundo real, desde la trayectoria de un proyectil hasta la forma de un arco arquitectónico. Comprender sus componentes y cómo se grafica una parábola es crucial para su aplicación.