Definicion De Una Funcion De Varias Variables

Analizar y resolver problemas relacionados con la definición de una función de varias variables requiere una estrategia clara y metódica. Empezaremos descomponiendo el problema en partes manejables.
Entender la Definición Base
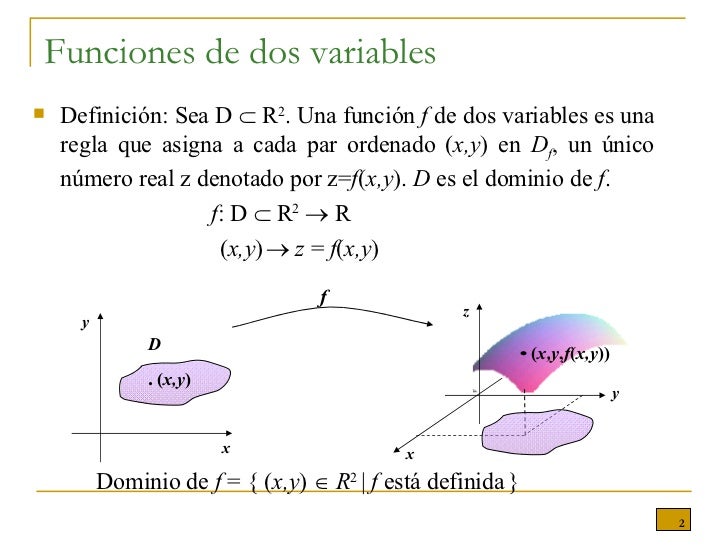
Primero, asegurémonos de entender qué es una función de varias variables. Se trata de una regla que asigna un único valor a cada punto en un subconjunto de un espacio n-dimensional. Este espacio se denota generalmente como Rn, donde n es el número de variables independientes. La función misma se representa comúnmente como f(x1, x2, ..., xn).
La clave es identificar el dominio y rango de la función. El dominio es el conjunto de todas las entradas posibles (los puntos en Rn). El rango es el conjunto de todos los valores de salida posibles. Visualizar estos conjuntos ayuda a comprender el comportamiento de la función.
Identificar los Supuestos Implícitos
Muchos problemas asumen ciertas propiedades de la función. Por ejemplo, se asume que la función es continua o diferenciable en su dominio. Estos supuestos son importantes porque influyen en las técnicas que podemos usar para analizar la función. Un análisis crítico implica reconocer estos supuestos.
Considera si el dominio está restringido. ¿Existen limitaciones específicas en los valores que las variables pueden tomar? Estas restricciones pueden ser explícitas (dadas en el problema) o implícitas (por ejemplo, el denominador de una fracción no puede ser cero). Identificar estas restricciones es crucial para evitar errores.
Evaluar las Opciones de Solución
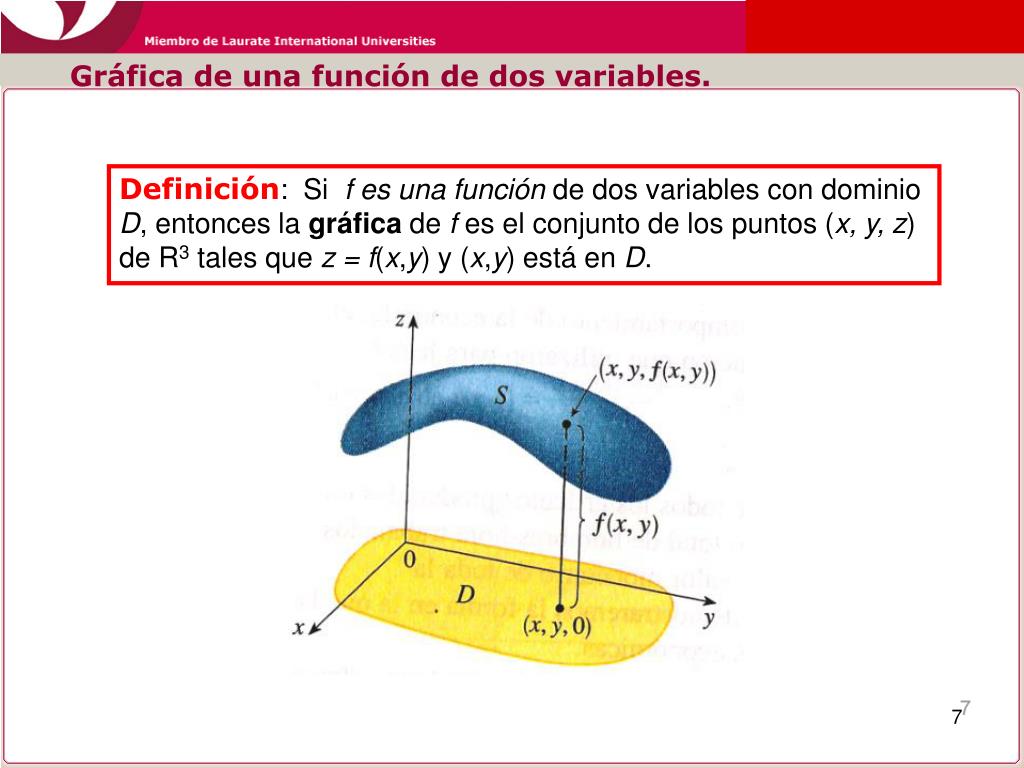
Una vez que entendemos la definición y los supuestos, podemos explorar las opciones de solución. Dependiendo del problema, esto podría implicar graficar la función. Podría también involucrar el cálculo de derivadas parciales, o la optimización de la función sujeta a ciertas restricciones. Cada opción tiene sus propias ventajas y desventajas.
El cálculo de derivadas parciales es útil para encontrar puntos críticos. Estos puntos son donde la función puede tener un máximo, un mínimo o un punto de silla. Analizar la matriz Hessiana en estos puntos nos ayuda a determinar la naturaleza de estos extremos. Recuerda que este método asume que la función es diferenciable.
Para la optimización con restricciones, podemos usar el método de los multiplicadores de Lagrange. Este método nos permite encontrar los puntos donde la función alcanza su máximo o mínimo sujeto a una o más restricciones. La formulación correcta de la función Lagrangiana es vital para obtener resultados precisos.
Dibujar Conclusiones Razonadas
Después de aplicar una o más técnicas, debemos interpretar los resultados. ¿Los resultados son consistentes con los supuestos iniciales? ¿Tienen sentido en el contexto del problema?
Verifica tus resultados. Si es posible, usa un software de cálculo para confirmar tus cálculos. Una pequeña equivocación en las derivadas o integrales puede llevar a conclusiones incorrectas. La verificación cruzada con otras personas también es valiosa.
Finalmente, expresa tus conclusiones de manera clara y concisa. Resume los pasos clave que seguiste y justifica tus respuestas. Una buena explicación demuestra una comprensión profunda del tema. Recuerda que la claridad y la precisión son esenciales en cualquier análisis matemático.