Distribucion De Frecuencias Para Variables Cuantitativas

¡Hola estudiantes! Vamos a sumergirnos en un tema fundamental de la estadística: la Distribución de Frecuencias para Variables Cuantitativas. No se preocupen, lo haremos paso a paso para que todo quede claro. ¡Ánimo!

¿Qué es una Variable Cuantitativa?

Primero, recordemos qué es una variable cuantitativa. Es aquella que se puede expresar numéricamente. Piensen en la edad, la altura, el peso, el número de hijos, o la temperatura. Todas estas se miden con números.

Estas variables se dividen en dos tipos: discretas y continuas. Las discretas toman valores enteros (número de hijos). Las continuas pueden tomar cualquier valor dentro de un rango (altura, peso).

¿Qué es una Distribución de Frecuencias?

Una distribución de frecuencias es una tabla o gráfico que organiza un conjunto de datos. Muestra cuántas veces aparece cada valor (o rango de valores) en la muestra. En otras palabras, nos dice la frecuencia con la que se observa cada dato.

Imaginemos que tenemos las edades de 20 estudiantes. Una distribución de frecuencias nos mostraría cuántos estudiantes tienen 18 años, cuántos 19, cuántos 20, y así sucesivamente.

Tipos de Frecuencias

Hay diferentes tipos de frecuencias que debemos conocer:

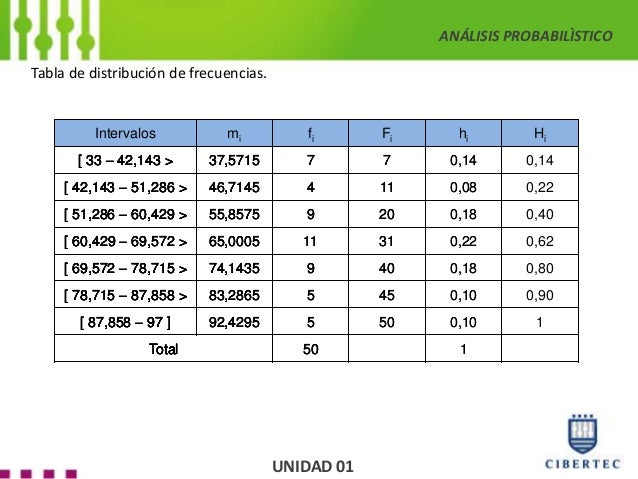
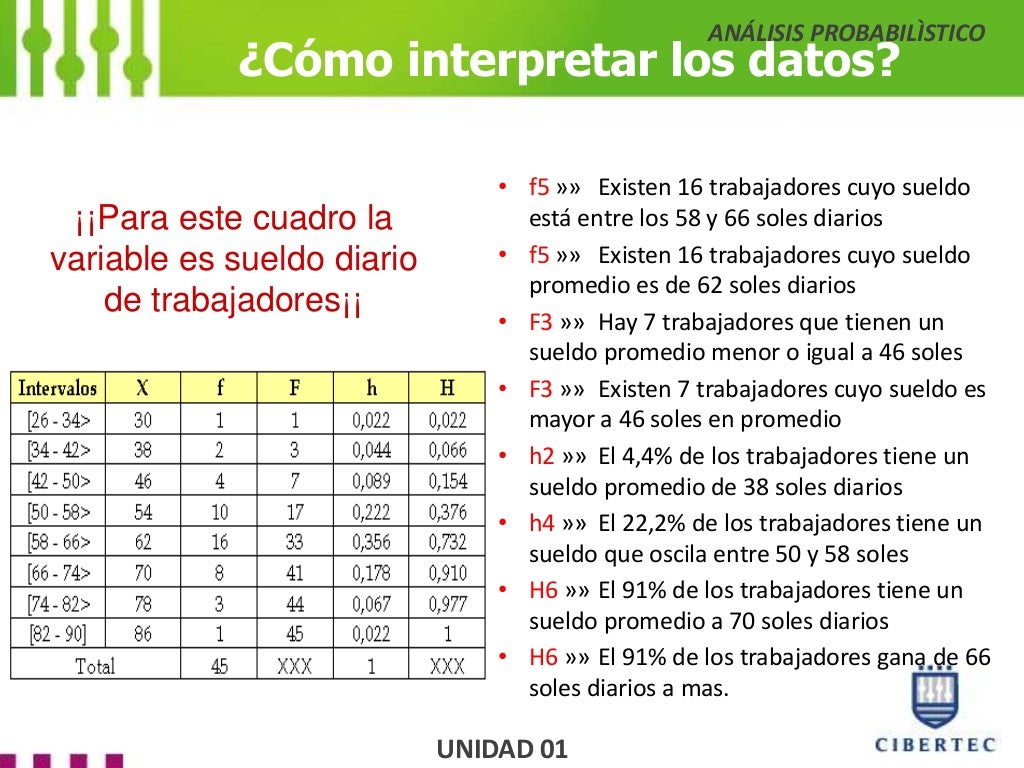
Frecuencia Absoluta (f_i): Es el número de veces que aparece un valor específico. Por ejemplo, si 5 estudiantes tienen 19 años, la frecuencia absoluta para la edad de 19 es 5.
Frecuencia Relativa (h_i): Es la proporción de veces que aparece un valor. Se calcula dividiendo la frecuencia absoluta entre el número total de datos. h_i = f_i / N (donde N es el tamaño de la muestra).
Frecuencia Acumulada Absoluta (F_i): Es la suma de las frecuencias absolutas hasta un valor específico. Nos dice cuántos datos son menores o iguales a ese valor.
Frecuencia Acumulada Relativa (H_i): Es la suma de las frecuencias relativas hasta un valor específico. Nos dice la proporción de datos que son menores o iguales a ese valor.

Construyendo una Distribución de Frecuencias (Datos No Agrupados)

Para datos no agrupados (donde los valores son distintos y no necesitan agruparse en intervalos), la tabla es sencilla. Primero, listamos todos los valores únicos de la variable. Luego, contamos la frecuencia absoluta de cada valor. Finalmente, calculamos las frecuencias relativas y acumuladas si es necesario.

Por ejemplo, si tenemos las edades: 18, 19, 18, 20, 19, 18, 21, 19, 20, 18... La tabla mostraría la frecuencia de cada edad individualmente.

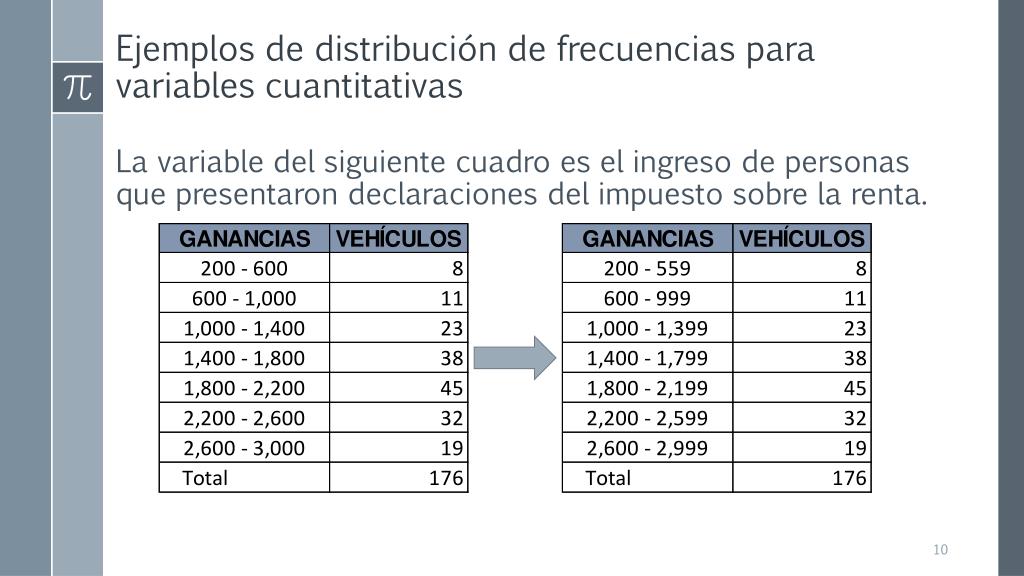
Construyendo una Distribución de Frecuencias (Datos Agrupados)

Cuando tenemos muchos valores distintos o datos continuos, es útil agruparlos en intervalos de clase. Esto simplifica la presentación y el análisis.

Para crear los intervalos, debemos determinar el rango de los datos (valor máximo - valor mínimo). Luego, decidimos el número de intervalos (generalmente entre 5 y 15). El ancho del intervalo se calcula dividiendo el rango entre el número de intervalos.

Cada intervalo tiene un límite inferior y un límite superior. Debemos asegurarnos de que los intervalos no se solapen y que cubran todos los valores de los datos.

Una vez definidos los intervalos, contamos cuántos datos caen dentro de cada uno (frecuencia absoluta). Después, calculamos las demás frecuencias (relativa, acumulada).

Representaciones Gráficas

Las distribuciones de frecuencias se pueden representar gráficamente. Para datos no agrupados, podemos usar un diagrama de barras. Para datos agrupados, un histograma es muy útil. El histograma muestra las frecuencias de cada intervalo como la altura de las barras.

También podemos usar un polígono de frecuencias, que es una línea que conecta los puntos medios de cada barra del histograma.