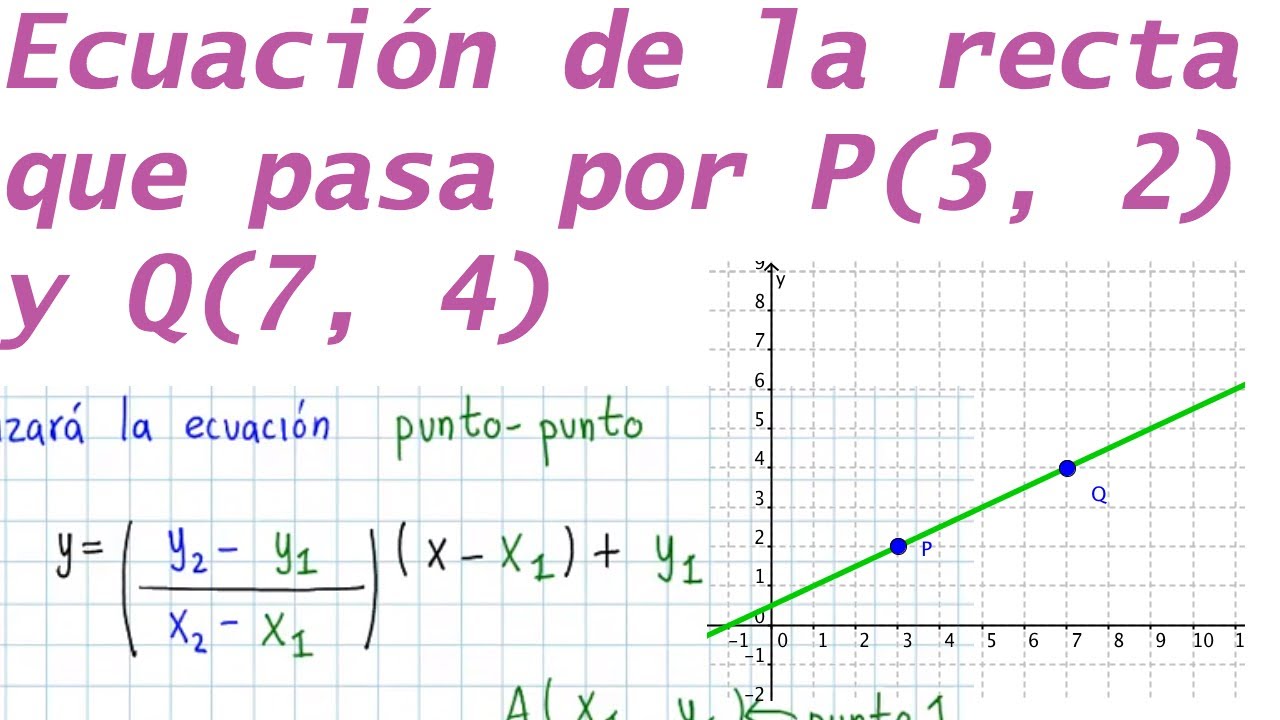
Ecuacion De La Recta Que Pasa Por Dos Puntos

Vamos a encontrar la ecuación de la recta que pasa por dos puntos dados. Usaremos un enfoque paso a paso. Esto facilitará la comprensión del proceso.
Paso 1: Identificar los Puntos Dados
Primero, identifica los dos puntos. Llamémoslos P1(x1, y1) y P2(x2, y2). Es crucial tener estos valores claramente definidos. Por ejemplo, si tenemos los puntos (1, 2) y (3, 4), entonces x1 = 1, y1 = 2, x2 = 3, y2 = 4.
Paso 2: Calcular la Pendiente (m)
La pendiente, representada por m, es un valor importante. Se calcula usando la fórmula: m = (y2 - y1) / (x2 - x1). Sustituye los valores de los puntos en esta fórmula. Asegúrate de restar en el orden correcto.
Usando nuestro ejemplo anterior (1, 2) y (3, 4), calculamos la pendiente: m = (4 - 2) / (3 - 1) = 2 / 2 = 1. Por lo tanto, la pendiente es 1. La pendiente describe la inclinación de la recta.
Paso 3: Usar la Forma Punto-Pendiente
La forma punto-pendiente es útil para encontrar la ecuación de la recta. Esta forma se escribe como: y - y1 = m(x - x1). Necesitamos la pendiente (m) y uno de los puntos (x1, y1).
En nuestro ejemplo, ya tenemos la pendiente m = 1. Podemos usar el punto (1, 2) como (x1, y1). Sustituye estos valores en la forma punto-pendiente: y - 2 = 1(x - 1). Esta es una representación de la ecuación de la recta.
Paso 4: Simplificar la Ecuación (Forma Pendiente-Ordenada al Origen)
Normalmente, queremos la ecuación en la forma pendiente-ordenada al origen. Esta forma es y = mx + b, donde b es la ordenada al origen. Simplificaremos la ecuación obtenida en el paso anterior.
Empezamos con y - 2 = 1(x - 1). Distribuimos el 1: y - 2 = x - 1. Luego, sumamos 2 a ambos lados: y = x - 1 + 2. Finalmente, simplificamos: y = x + 1. Esta es la ecuación de la recta en la forma pendiente-ordenada al origen.
Paso 5: Verificar la Solución
Es recomendable verificar que ambos puntos originales satisfacen la ecuación obtenida. Sustituye las coordenadas de cada punto en la ecuación y = x + 1.
Para el punto (1, 2): 2 = 1 + 1, lo cual es cierto. Para el punto (3, 4): 4 = 3 + 1, que también es cierto. Esto confirma que nuestra ecuación es correcta. Si alguno de los puntos no cumple la ecuación, revisa tus cálculos.
Resumen
Hemos seguido un proceso metódico. Primero, identificamos los puntos. Luego, calculamos la pendiente. Usamos la forma punto-pendiente y simplificamos a la forma pendiente-ordenada al origen. Finalmente, verificamos la solución. Siguiendo estos pasos, puedes encontrar la ecuación de cualquier recta que pasa por dos puntos dados.
Recuerda que el orden de los puntos en el cálculo de la pendiente es importante. Mantén la consistencia. También, ten cuidado con los signos negativos al sustituir valores. Una práctica cuidadosa conduce a resultados precisos.