Ejercicios De Estadistica Descriptiva Datos Agrupados

Ejercicios de Estadística Descriptiva con Datos Agrupados se refieren a la aplicación de métodos estadísticos para resumir y describir un conjunto de datos que han sido organizados en intervalos o clases, en lugar de analizar datos individuales. ¡Vamos a entenderlo mejor!

¿Qué son Datos Agrupados?

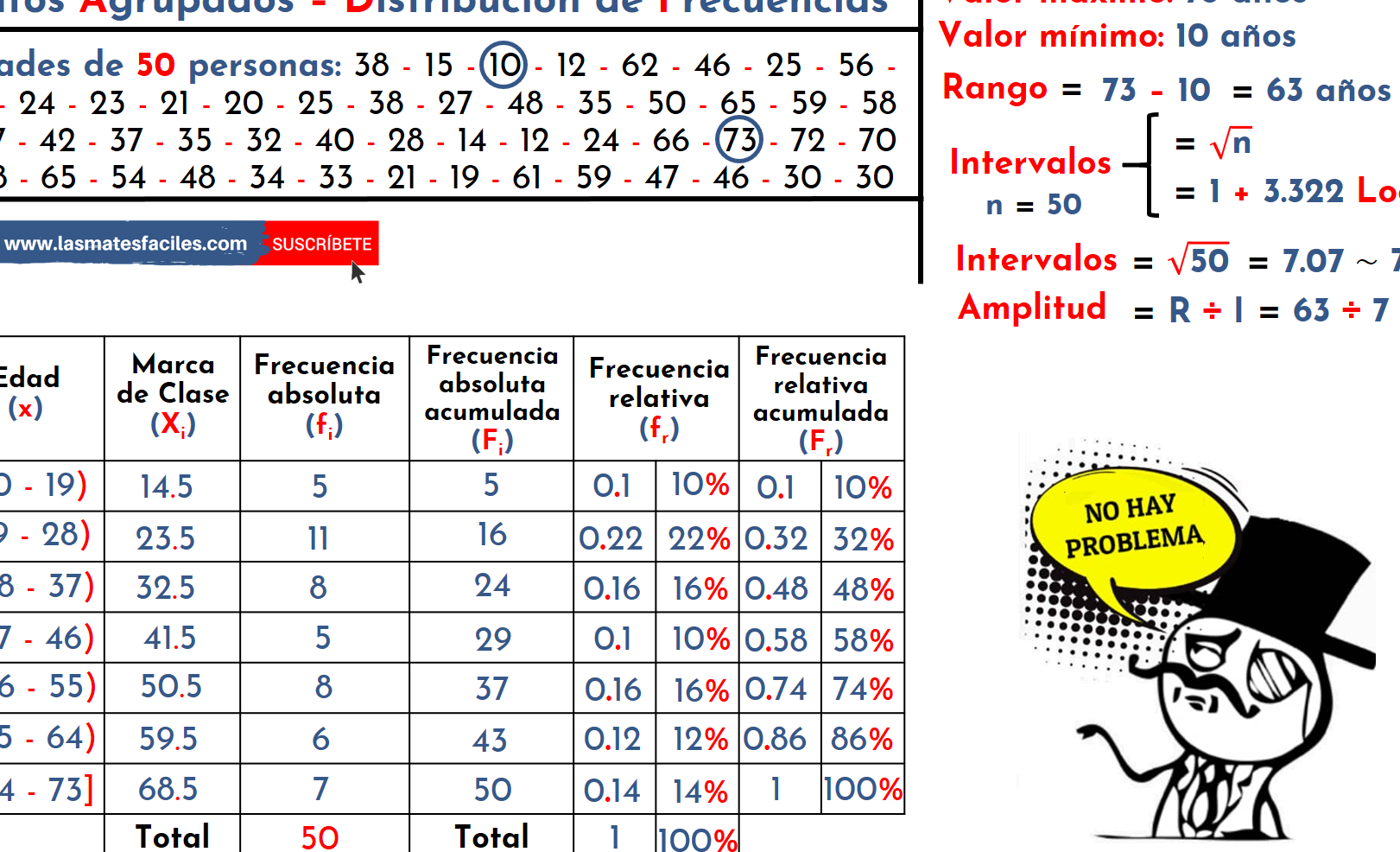
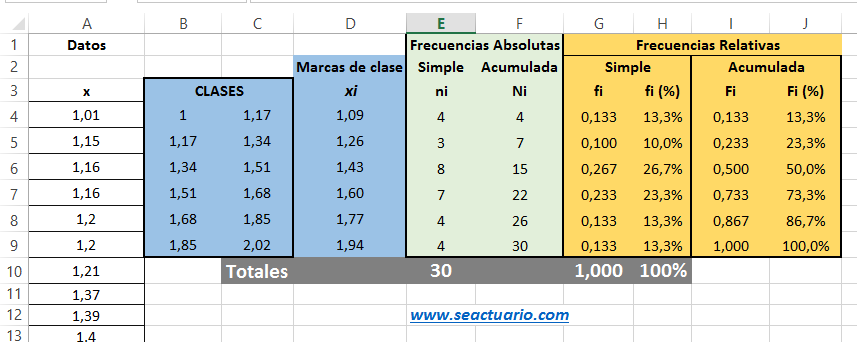
Imagina que tienes las edades de 100 personas. En lugar de tener una lista de 100 números diferentes, puedes agruparlos en rangos de edad, por ejemplo, de 20-30 años, de 30-40 años, etc. Cada rango es un intervalo de clase. La cantidad de personas en cada intervalo es la frecuencia.

Trabajar con datos agrupados facilita el análisis cuando tienes una gran cantidad de información. Es más sencillo visualizar tendencias y patrones.

Medidas de Tendencia Central para Datos Agrupados

Las medidas de tendencia central nos dan una idea del "centro" de los datos. Las más comunes son:

Media: Se calcula encontrando el punto medio de cada intervalo (marca de clase), multiplicándolo por su frecuencia, sumando todos los resultados y dividiendo por el número total de datos. Piensa en ello como un promedio ponderado.
Mediana: Es el valor que se encuentra en el "medio" de los datos. En datos agrupados, se encuentra el intervalo que contiene la mediana, y luego se aplica una fórmula para estimar su valor preciso dentro de ese intervalo.
Moda: Es el intervalo con la mayor frecuencia. Se le llama clase modal.

Medidas de Dispersión para Datos Agrupados

Las medidas de dispersión nos dicen qué tan "dispersos" están los datos alrededor del centro. Las más usadas son:

Rango: La diferencia entre el límite superior del último intervalo y el límite inferior del primer intervalo. Es una medida simple, pero sensible a valores extremos.
Varianza: Mide la dispersión promedio de los datos alrededor de la media. Se calcula una varianza ponderada, considerando las frecuencias de cada intervalo.
Desviación Estándar: Es la raíz cuadrada de la varianza. Es más fácil de interpretar que la varianza porque está en las mismas unidades que los datos originales.

Ejemplo Sencillo

Supongamos que tenemos las siguientes edades agrupadas:

20-30 años: 25 personas
30-40 años: 40 personas
40-50 años: 20 personas
50-60 años: 15 personas

Para calcular la media, primero encontramos la marca de clase (punto medio) de cada intervalo: 25, 35, 45, 55. Luego, multiplicamos por la frecuencia y sumamos: (25*25) + (35*40) + (45*20) + (55*15) = 3500. Finalmente, dividimos por el número total de personas (100): 3500/100 = 35. ¡La media es 35 años!

¿Por qué es útil?

El análisis de datos agrupados es útil en muchas situaciones. Por ejemplo, en investigaciones de mercado, para analizar rangos de ingresos; en salud pública, para analizar rangos de edad afectados por una enfermedad; o en educación, para analizar rangos de notas en un examen. Proporciona una visión general y simplificada de conjuntos de datos complejos.

Recuerda, practicar con ejercicios es la mejor manera de dominar la estadística descriptiva con datos agrupados. ¡No te rindas!