Ejercicios Resueltos De Motores En Derivacion

¡Hola estudiantes! Hoy vamos a desentrañar los misterios de los motores en derivación. Estos motores, también conocidos como motores shunt, son esenciales en muchas aplicaciones industriales. Pero, ¿cómo resolvemos los ejercicios que los involucran? ¡Vamos paso a paso!

¿Qué es un Motor en Derivación?

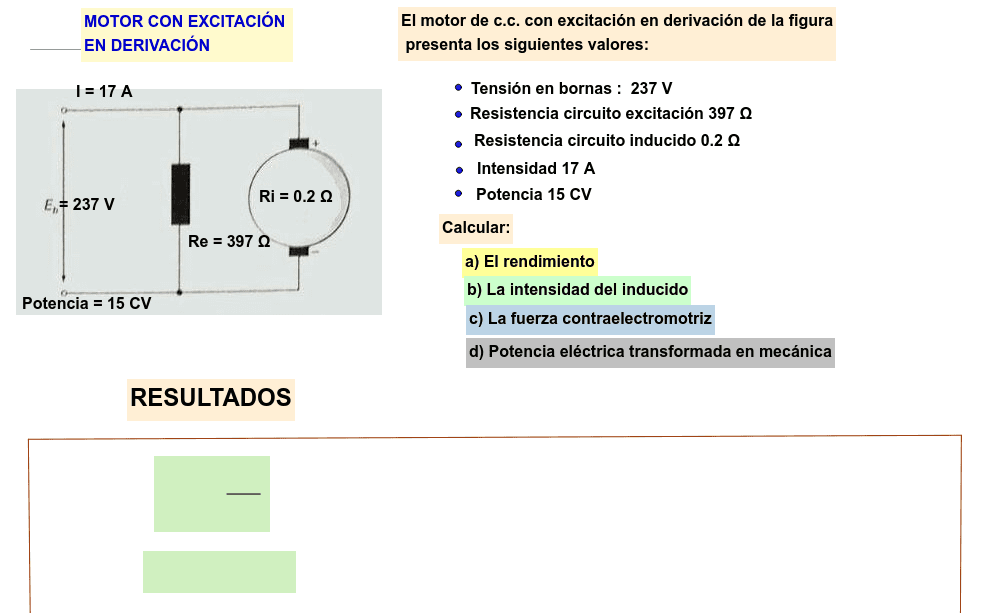
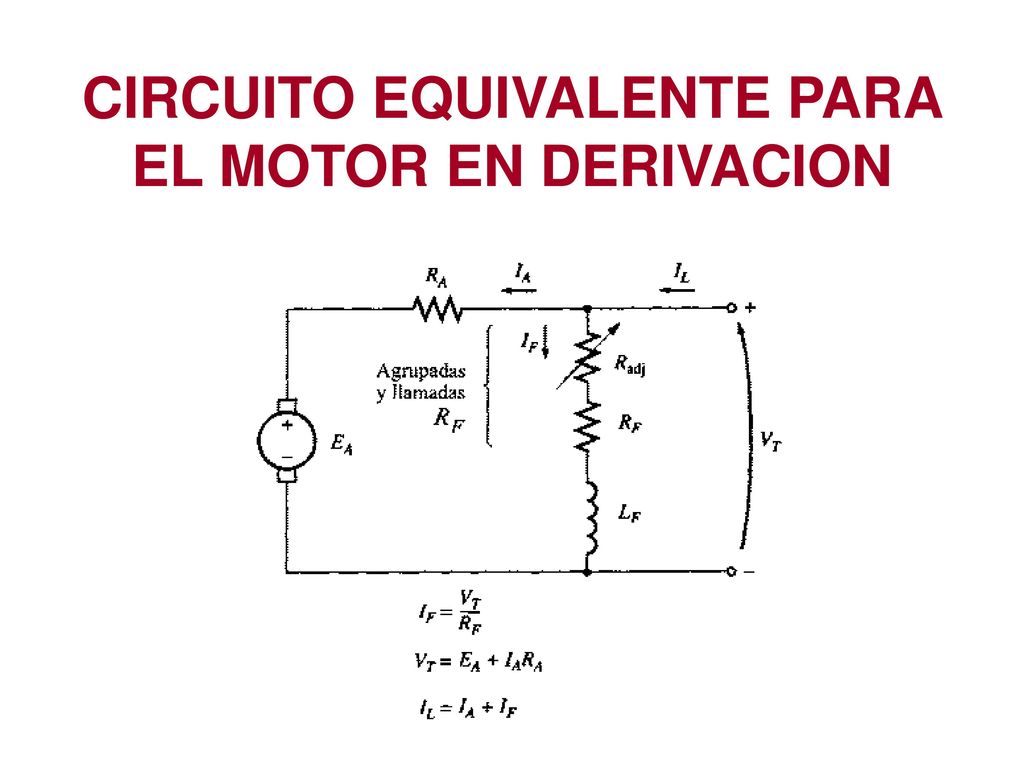
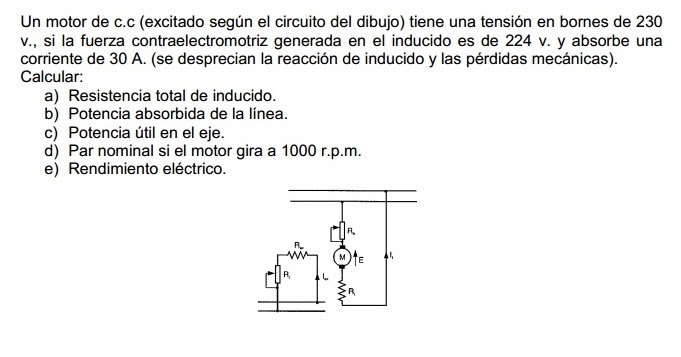
Un motor en derivación se caracteriza porque el bobinado del campo (el que crea el campo magnético) está conectado en paralelo o "en derivación" con el bobinado de la armadura (el que gira). Esto significa que la tensión aplicada al motor es la misma para ambos bobinados.

Fórmulas Clave

Para resolver ejercicios, necesitamos algunas fórmulas importantes:

Voltaje de armadura (Va): Va = V - Ia * Ra (donde V es el voltaje total, Ia es la corriente de armadura y Ra es la resistencia de la armadura).
Corriente de armadura (Ia): Ia = (V - Va) / Ra
Fuerza contraelectromotriz (E): E = K * Φ * ω (donde K es una constante, Φ es el flujo magnético y ω es la velocidad angular). Recuerda que E también es muy similar a Va en valor, normalmente ignorando las perdidas rotacionales.
Corriente de campo (If): If = V / Rf (donde Rf es la resistencia del campo).
Corriente total (I): I = Ia + If
Torque (T): T = K' * Φ * Ia (donde K' es otra constante).

Ejemplo Práctico: Paso a Paso

Imaginemos un motor en derivación con los siguientes datos:

Voltaje (V) = 220 V
Resistencia de armadura (Ra) = 0.5 Ω
Resistencia de campo (Rf) = 220 Ω
Corriente total (I) = 11 A

Nuestro objetivo: calcular la corriente de armadura (Ia) y la corriente de campo (If).

Paso 1: Calcular la Corriente de Campo (If)

Usamos la fórmula: If = V / Rf = 220 V / 220 Ω = 1 A

Paso 2: Calcular la Corriente de Armadura (Ia)

Usamos la fórmula: I = Ia + If. Entonces, Ia = I - If = 11 A - 1 A = 10 A

¡Listo! Hemos calculado la corriente de armadura y la corriente de campo.

Otro Ejemplo: Calculando la Fuerza Contraelectromotriz

Supongamos que en el ejemplo anterior, sabemos que la constante K * Φ = 0.2. Además, la velocidad angular ω = 100 rad/s. ¿Cuál es la fuerza contraelectromotriz (E)?

Usamos la fórmula: E = K * Φ * ω = 0.2 * 100 rad/s = 20 V.

Importante: La fuerza contraelectromotriz es crucial porque limita la corriente que circula por la armadura. Si la fuerza contraelectromotriz fuera cero (al arrancar el motor), la corriente sería enorme, pudiendo dañar el motor.

Consejos Finales

Siempre dibuja un esquema del circuito para visualizar mejor la conexión.
Identifica claramente los datos proporcionados y lo que se te pide calcular.
Utiliza las unidades correctas (voltios, amperios, ohmios, etc.).
Practica con diferentes ejercicios para familiarizarte con las fórmulas y conceptos.

Con práctica y paciencia, dominarás los ejercicios de motores en derivación. ¡No te rindas!