Escribe Tres Numeros Que Sean Primos Entre Si

¿Qué significa "Escribe tres números que sean primos entre sí"? En esencia, te están pidiendo que encuentres tres números que, aunque individualmente puedan o no ser primos, no compartan ningún factor común además del 1. Piensa en ello como un equipo: cada número tiene sus propias características, pero no hay un número más grande que 1 que divida a los tres.

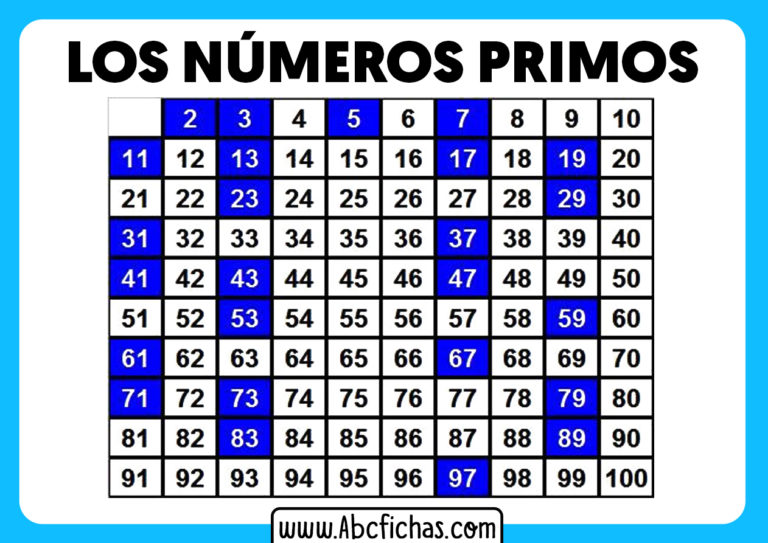
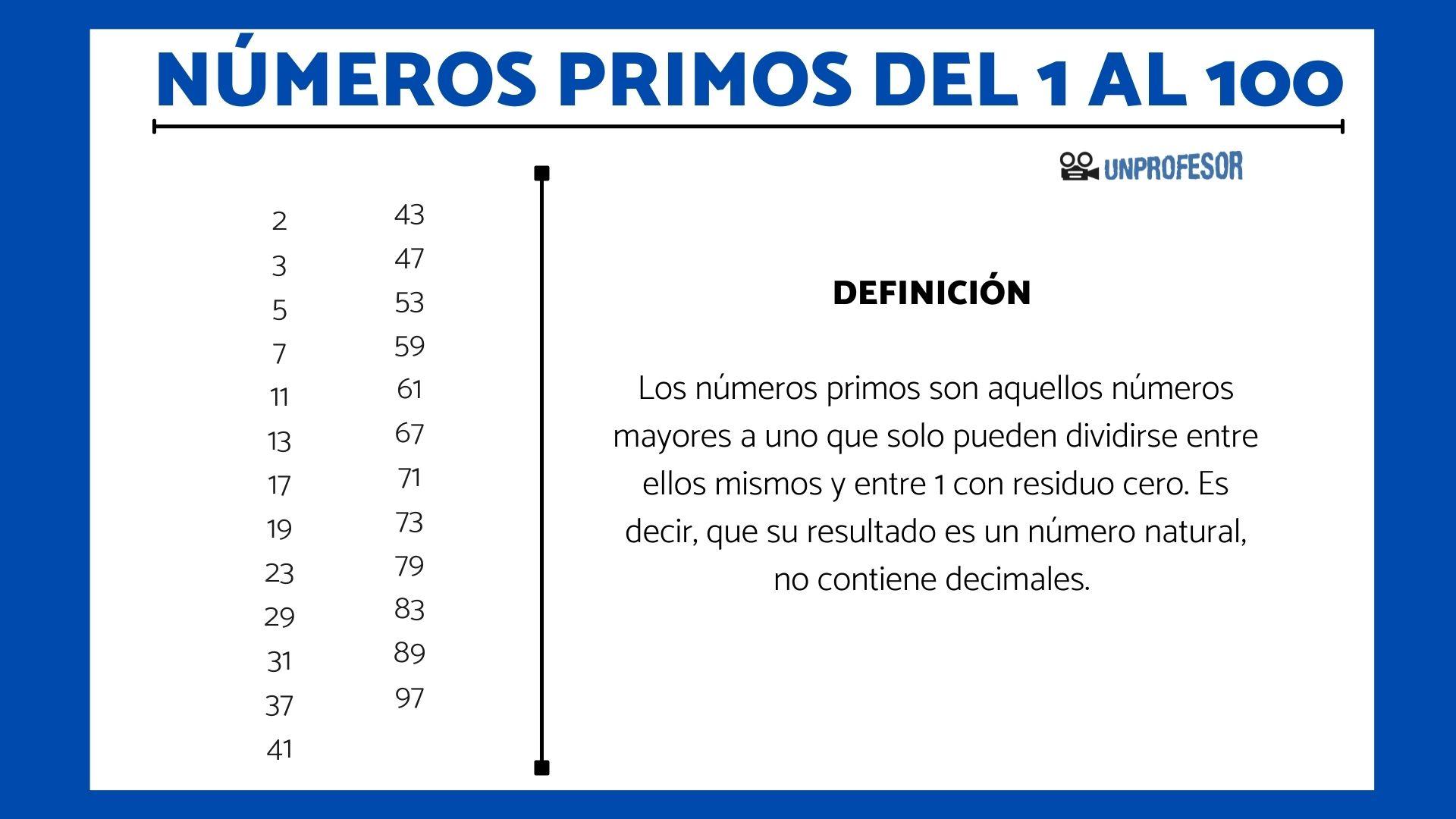
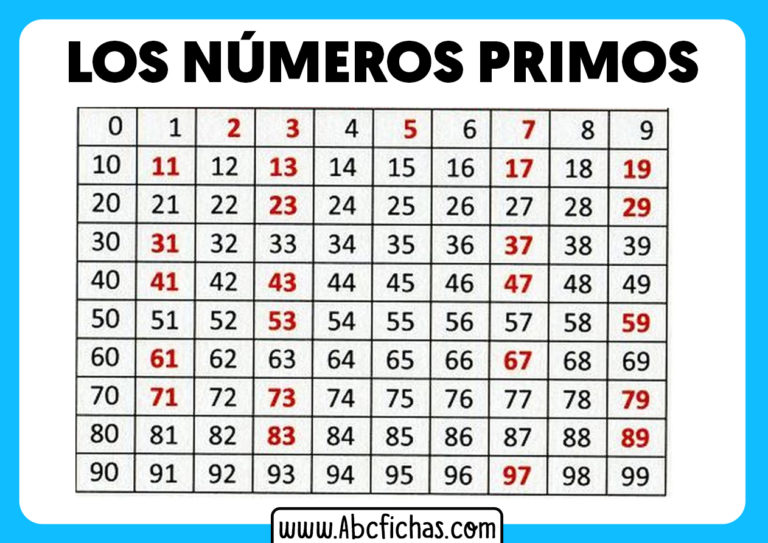
Definición clave: Números primos entre sí (también llamados coprimos) son aquellos cuyo máximo común divisor (MCD) es 1.

¿Cómo funciona? Para encontrar tres números primos entre sí, puedes seguir estos pasos:

1. Elige tres números cualesquiera: No importa si son pares, impares, primos o compuestos. Por ejemplo, podríamos elegir 6, 10 y 15.
2. Encuentra los factores de cada número:
   • 6: 1, 2, 3, 6
   • 10: 1, 2, 5, 10
   • 15: 1, 3, 5, 15
3. Identifica los factores comunes: ¿Comparten algún factor además del 1? En este caso, no hay un factor que divida a los tres números. Por ejemplo, 2 divide a 6 y 10, pero no a 15. 3 divide a 6 y 15, pero no a 10. Y 5 divide a 10 y 15, pero no a 6.
4. Conclusión: Como el único factor común a los tres números es 1, 6, 10 y 15 son primos entre sí.

Otro ejemplo: ¿Qué tal 8, 9 y 14?

• 8: 1, 2, 4, 8
• 9: 1, 3, 9
• 14: 1, 2, 7, 14

En este caso, aunque 8 y 14 comparten el factor 2, 9 no lo comparte. Por lo tanto, 8, 9 y 14 son primos entre sí.

¿Por qué importa? El concepto de números primos entre sí es fundamental en diversas áreas de las matemáticas, especialmente en:

• Teoría de números: Ayuda a comprender las propiedades y relaciones entre los números enteros.
• Criptografía: Se utiliza en algoritmos de encriptación para asegurar la información.
• Fracciones: Simplificar fracciones hasta su mínima expresión implica encontrar el máximo común divisor (MCD). Si el MCD entre el numerador y el denominador es 1, entonces ya son primos entre sí, y la fracción está simplificada.

En resumen, encontrar tres números primos entre sí es un ejercicio de identificar números que no comparten factores comunes, más allá de 1. Es un concepto clave con aplicaciones importantes en matemáticas y más allá.