Espacio De Estados A Funcion De Transferencia
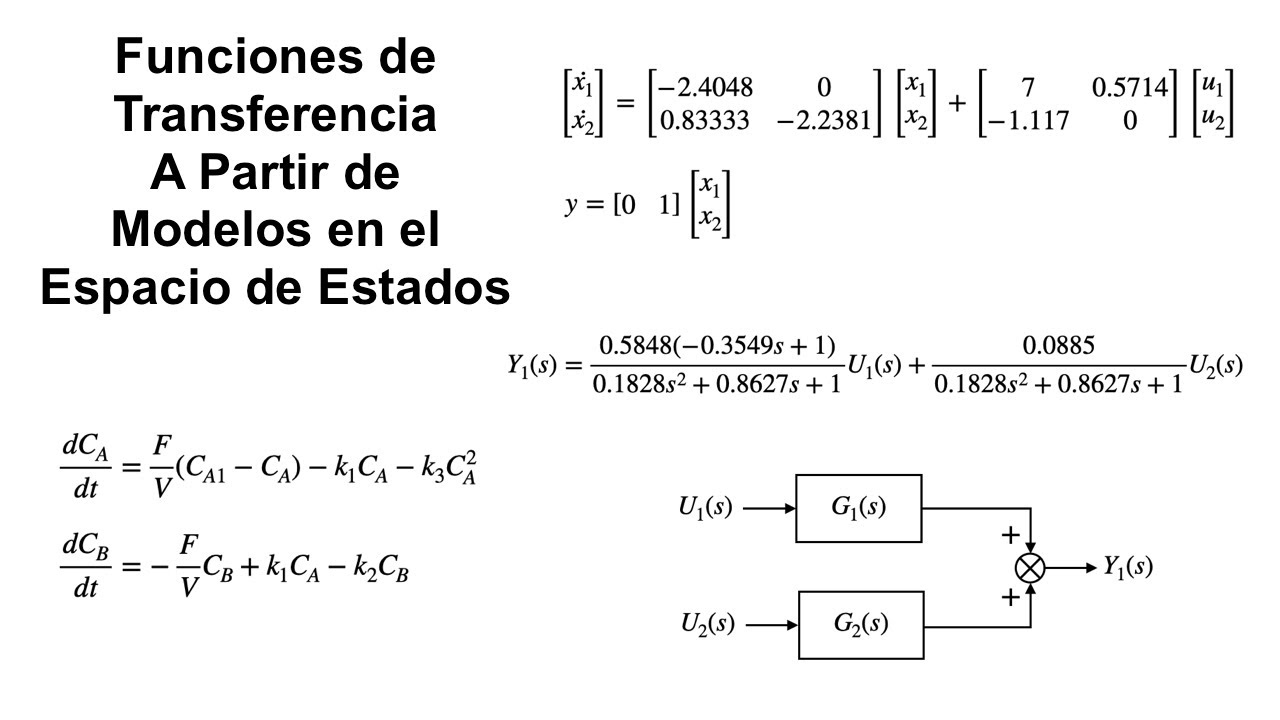
Comencemos con la conversión de un espacio de estados a una función de transferencia. Primero, identifiquemos la información clave proporcionada en el problema. Esta información generalmente incluye las matrices A, B, C y D.
Identificación de las Matrices del Espacio de Estados
Necesitamos identificar correctamente cada matriz. A es la matriz de estado. B es la matriz de entrada. C es la matriz de salida. D es la matriz de transmisión directa.
Verificamos las dimensiones de las matrices. Esto asegura la compatibilidad para las operaciones matriciales posteriores. Una dimensión incorrecta indica un posible error en la definición del sistema.
Calculando (sI - A)
El siguiente paso es calcular (sI - A). Aquí, s representa la variable de Laplace. I es la matriz identidad. La matriz identidad debe tener las mismas dimensiones que A.
Multiplicamos la matriz identidad I por s. Luego, restamos la matriz A del resultado. Esto da como resultado una nueva matriz en términos de s.
Calculando la Inversa de (sI - A)
Luego, calculamos la inversa de (sI - A). Esta es un paso crucial. La inversa a menudo se denota como (sI - A)-1.
Existen varios métodos para calcular la inversa de una matriz. Para matrices de 2x2, existe una fórmula directa. Para matrices más grandes, se pueden usar métodos como la adjunta y el determinante o métodos numéricos.
Multiplicando las Matrices
Una vez que tenemos (sI - A)-1, procedemos con la multiplicación de matrices. Calculamos C(sI - A)-1B. Este paso involucra multiplicación matricial estándar.
Asegúrate del orden correcto de la multiplicación. El orden de la multiplicación afecta el resultado final. La multiplicación de matrices no es conmutativa.
Sumando la Matriz de Transmisión Directa
Finalmente, sumamos la matriz de transmisión directa D. La función de transferencia G(s) se calcula como: G(s) = C(sI - A)-1B + D.
Este paso completa la conversión. G(s) representa la función de transferencia del sistema. Es la relación entre la salida y la entrada en el dominio de Laplace.
Simplificación y Análisis
Simplificamos la función de transferencia resultante. Esto puede implicar la combinación de términos similares. También, la factorización de polinomios es fundamental para una representación concisa.
Analizamos la función de transferencia obtenida. Identificamos polos y ceros. Estos polos y ceros pueden proporcionar información sobre la estabilidad y el comportamiento del sistema.
Considera la posibilidad de realizar comprobaciones de validez. Por ejemplo, compara la respuesta en el dominio del tiempo obtenida de la función de transferencia con la respuesta en el dominio del tiempo simulada del espacio de estados original.
Consideraciones Adicionales
En algunos casos, la matriz D es cero. Esto simplifica el cálculo de la función de transferencia. Cuando D = 0, la función de transferencia se reduce a G(s) = C(sI - A)-1B.
Si el sistema tiene múltiples entradas y salidas, la función de transferencia será una matriz. Cada elemento de la matriz representa la función de transferencia entre una entrada específica y una salida específica.
La conversión de espacio de estados a función de transferencia es una herramienta poderosa. Permite analizar y diseñar sistemas de control utilizando técnicas de dominio de la frecuencia. Recuerda, la práctica constante es clave para dominar este proceso.








