Extremos Absolutos Y Relativos De Una Funcion

Vamos a explorar los extremos absolutos y relativos de una función. ¿Qué son? Son los puntos más altos (máximos) y más bajos (mínimos) que alcanza una función, ya sea en todo su dominio (absolutos) o en una zona específica (relativos).

Máximos y Mínimos: ¿Qué son?

Imagina una montaña rusa. Los puntos más altos son los máximos y los más bajos, los mínimos. En matemáticas, es lo mismo, pero con una función.

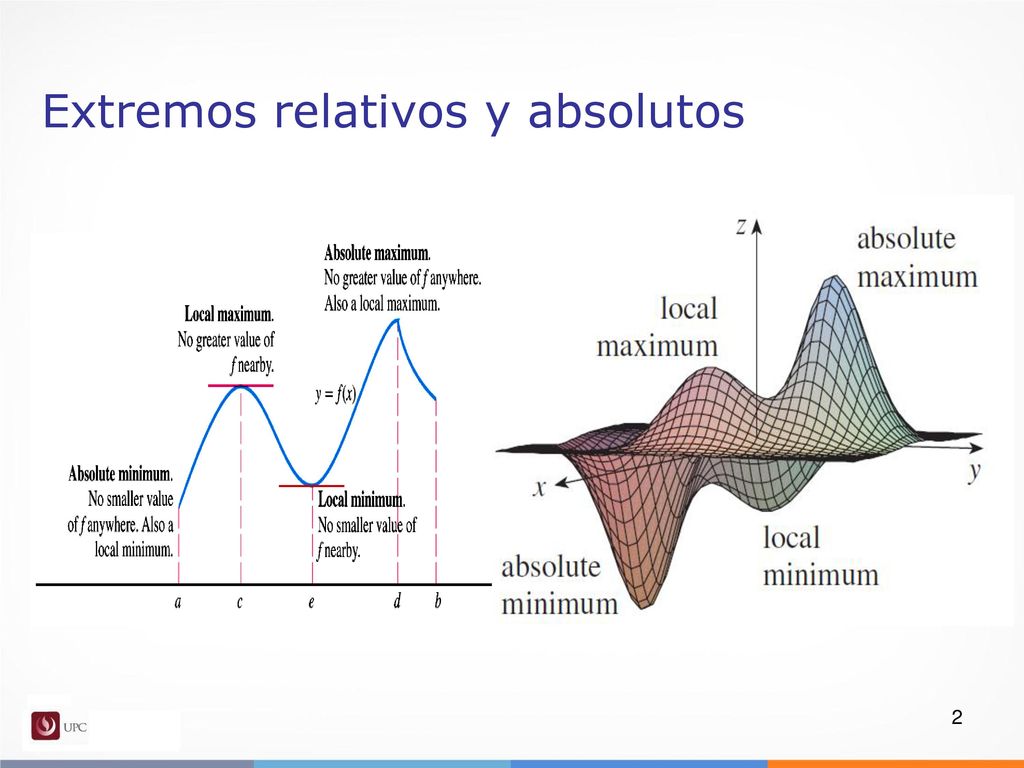
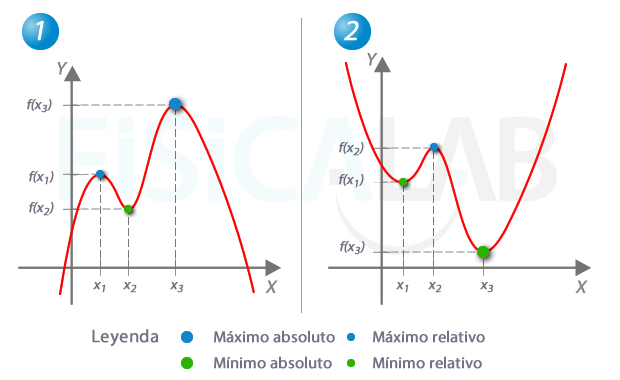
Extremo Absoluto: El punto más alto o más bajo de *toda* la función. Es el valor máximo o mínimo que la función toma en su dominio completo. Piensa en la cima más alta de *todo* el mundo. Es *el* máximo absoluto.

Extremo Relativo (o Local): El punto más alto o más bajo en una *zona* específica de la función. Es un máximo o mínimo dentro de un intervalo. Como la cima más alta de una *región* particular. Puede haber varios máximos y mínimos relativos.

Cómo Encontrarlos: Paso a Paso

Aquí te explicamos cómo encontrar estos puntos clave:

1. Encontrar la Derivada: Calcula la primera derivada de la función, f'(x). La derivada nos da la pendiente de la función en cada punto.
2. Puntos Críticos: Iguala la derivada a cero (f'(x) = 0). Las soluciones son los puntos críticos. Estos puntos son candidatos a ser máximos o mínimos (relativos). También busca puntos donde la derivada no existe (por ejemplo, en funciones con "picos").
3. Segunda Derivada (o Criterio de la Primera Derivada):
   • Segunda Derivada: Calcula la segunda derivada, f''(x). Evalúa la segunda derivada en cada punto crítico.
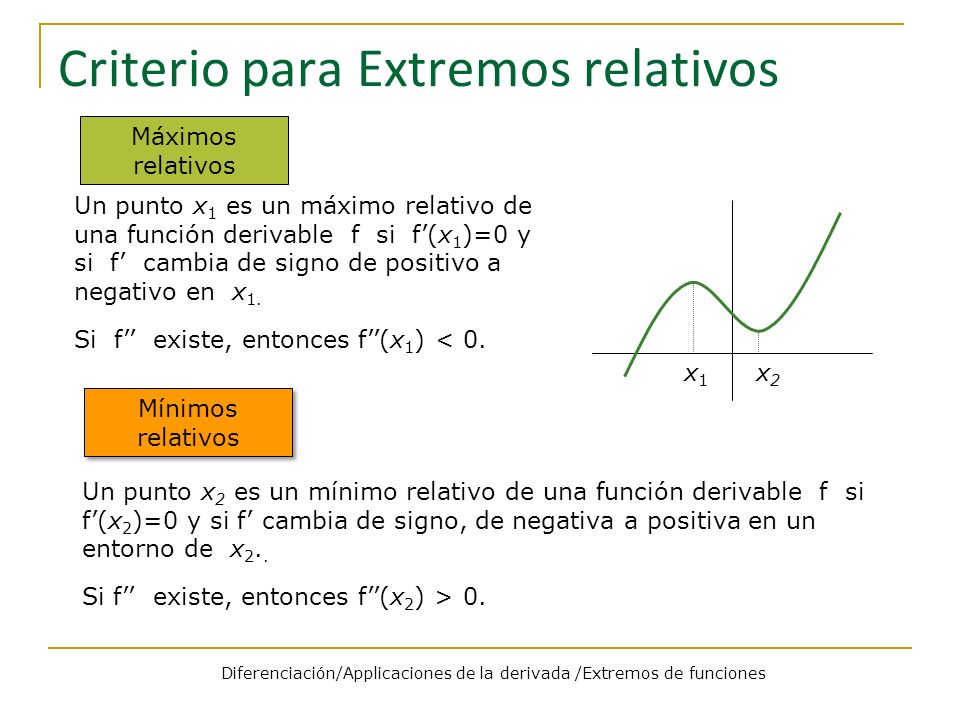
     • Si f''(x) > 0, es un mínimo relativo. (La función es cóncava hacia arriba)
     • Si f''(x) < 0, es un máximo relativo. (La función es cóncava hacia abajo)
     • Si f''(x) = 0, el criterio no decide, y necesitamos usar otro método.
   • Criterio de la Primera Derivada: Analiza el signo de la primera derivada *antes y después* del punto crítico. Si cambia de positivo a negativo, es un máximo; si cambia de negativo a positivo, es un mínimo.
4. Extremos Absolutos: Si estás buscando extremos absolutos en un intervalo cerrado [a, b], evalúa la función original f(x) en:
   • Los puntos críticos dentro del intervalo.
   • Los extremos del intervalo (a y b).
   El valor más grande es el máximo absoluto y el valor más pequeño es el mínimo absoluto.

Ejemplo Sencillo

Consideremos la función f(x) = x². Su derivada es f'(x) = 2x. Igualando a cero, 2x = 0, tenemos el punto crítico x = 0.

La segunda derivada es f''(x) = 2. Como f''(0) = 2 > 0, tenemos un mínimo relativo en x = 0. En este caso, también es el mínimo absoluto de la función.

¡Importante!

No todas las funciones tienen extremos absolutos o relativos. ¡Presta atención al dominio de la función y a los intervalos que te den!

Entender los extremos absolutos y relativos te ayuda a analizar el comportamiento de una función, resolver problemas de optimización y modelar situaciones del mundo real. ¡Sigue practicando!