Interpretacion Geometrica De Incrementos Y Diferenciales

¡Hola! Vamos a explorar la interpretación geométrica de incrementos y diferenciales. No te preocupes, suena complicado, pero lo haremos sencillo. Imagina que estás caminando por una calle. Eso es todo lo que necesitas saber por ahora.

Incrementos: ¡Cambios en la Vida Real!

Un incremento es simplemente un cambio. Es la diferencia entre dónde estás ahora y dónde estabas antes. Piénsalo como cuánto avanzaste al caminar por esa calle.

Imagina que estás en la posición x = 2 metros y luego te mueves a la posición x = 5 metros. El incremento en tu posición, que denotamos como Δx (Delta x), es: Δx = 5 - 2 = 3 metros. Avanzaste 3 metros. Fácil, ¿verdad?

Ahora, pensemos en altura. Si una planta mide 10 cm y crece hasta 15 cm, el incremento en su altura (Δy) es Δy = 15 - 10 = 5 cm. Creció 5 cm.

Incrementos en un Gráfico

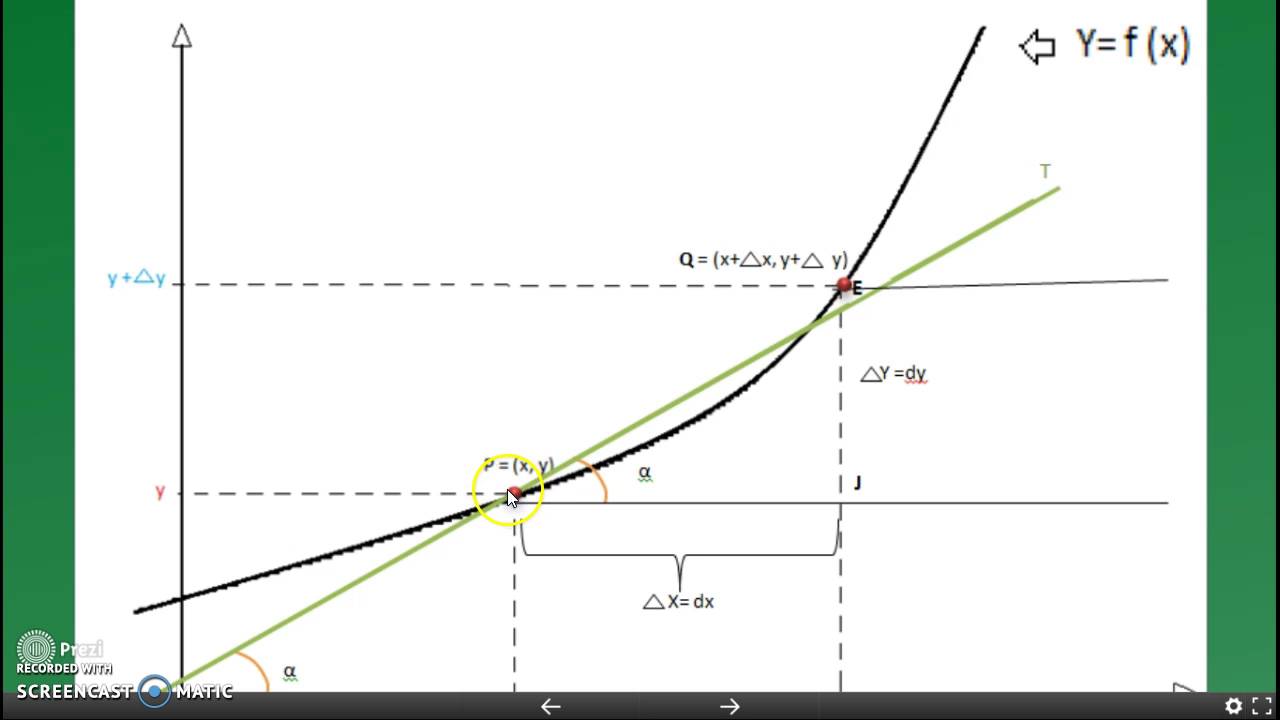
Visualicemos esto en un gráfico. Tenemos un eje horizontal (el eje x) y un eje vertical (el eje y). Imagina una función que dibuja una línea o curva en este gráfico. Esa línea representa una relación entre x e y.

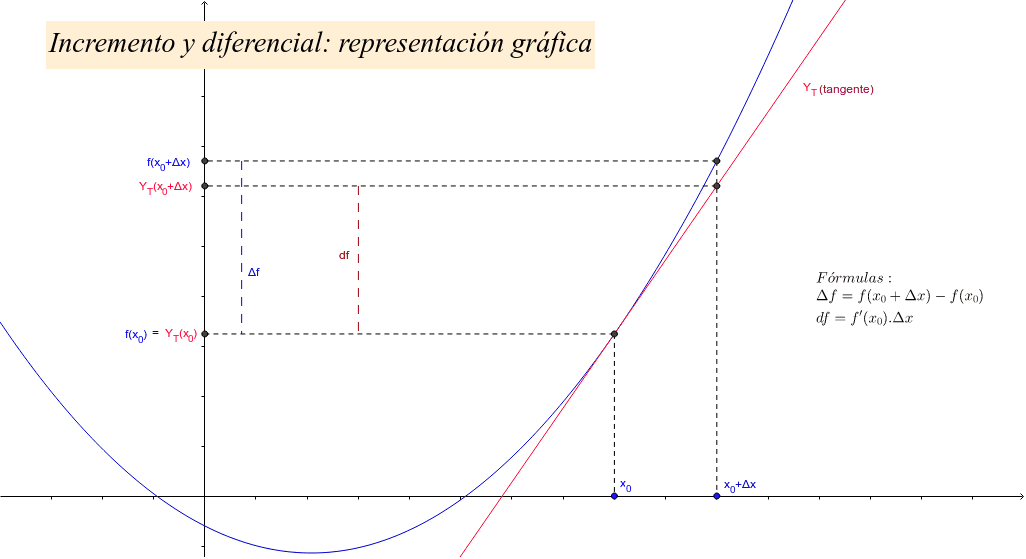
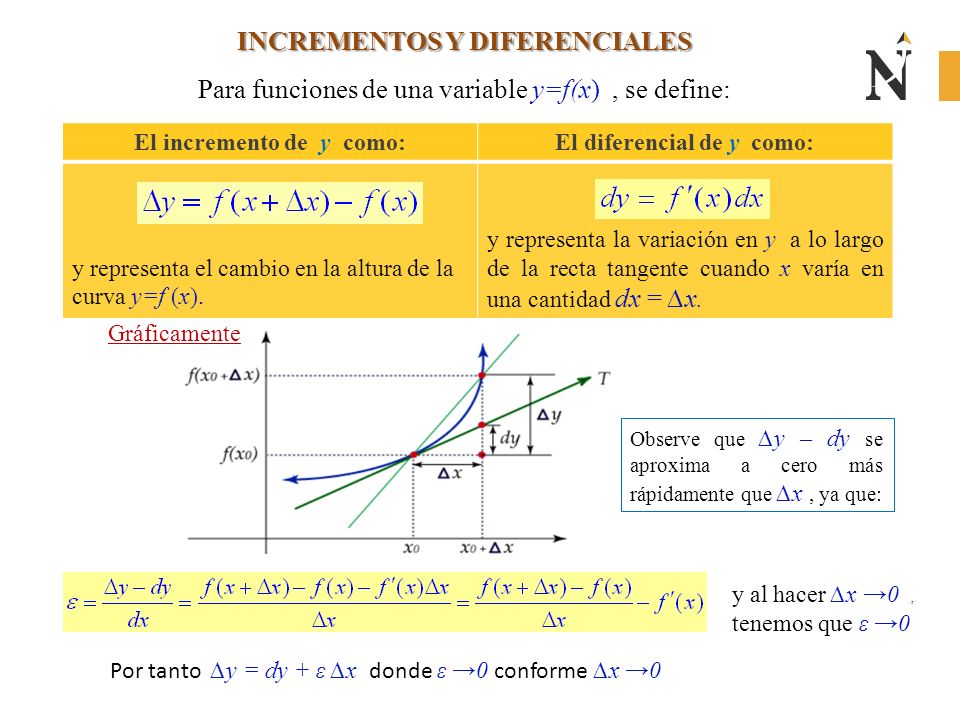
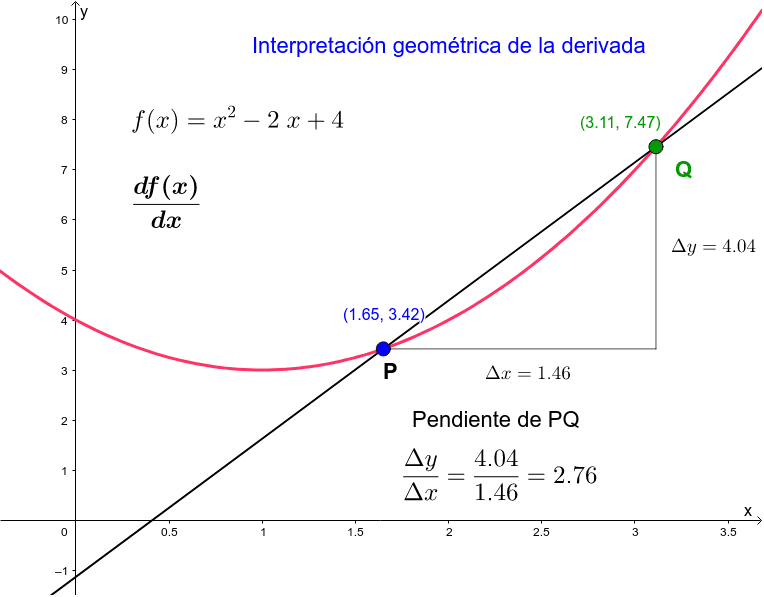
Si elegimos dos puntos en el eje x, digamos x₁ y x₂, podemos encontrar los correspondientes valores de y en la función: y₁ y y₂. El incremento en x es Δx = x₂ - x₁. El incremento en y es Δy = y₂ - y₁. Δx es el cambio horizontal y Δy es el cambio vertical.

En el gráfico, Δx es la distancia horizontal entre los dos puntos, y Δy es la distancia vertical. La relación Δy/Δx representa la pendiente de la línea que conecta esos dos puntos. La pendiente es la inclinación de la línea.

Diferenciales: Incrementos Infinitesimales

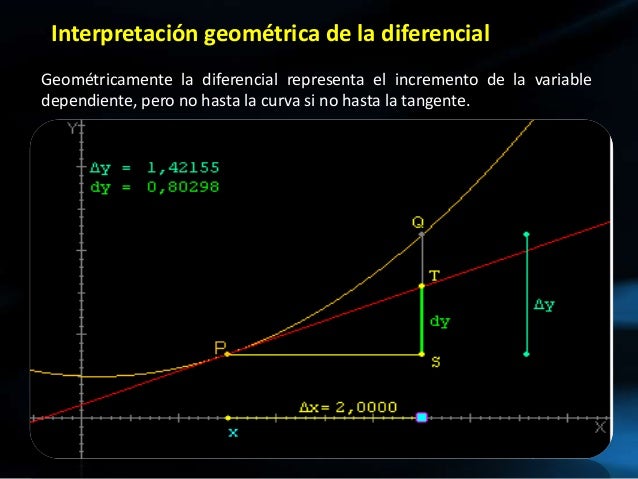
Ahora viene la parte un poco más abstracta: los diferenciales. Un diferencial es un incremento infinitesimalmente pequeño. Imagina que en lugar de dar un paso grande de 3 metros, das un paso tan pequeño que es casi cero.

Denotamos el diferencial de x como dx, y el diferencial de y como dy. Piensa en dx como un Δx que se ha hecho increíblemente pequeño, acercándose a cero. Lo mismo ocurre con dy respecto a Δy.

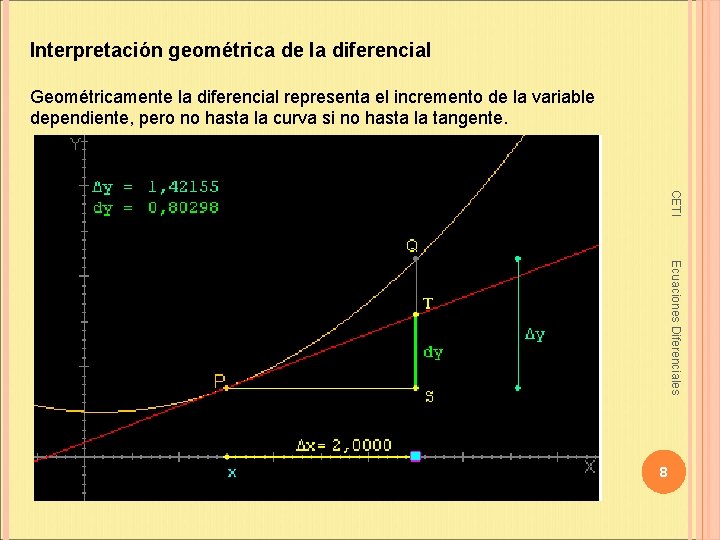
¿Por qué necesitamos algo tan pequeño? Porque nos permite analizar la función con gran precisión. Si tenemos una función y = f(x), entonces dy/dx representa la derivada de la función en un punto específico. La derivada es la pendiente de la línea tangente a la curva en ese punto.

Diferenciales y la Línea Tangente

La línea tangente es una línea que toca la curva en un solo punto. Su pendiente nos da la dirección instantánea de la curva en ese punto. El diferencial dy representa el cambio en y a lo largo de esa línea tangente, cuando x cambia por una cantidad infinitesimal dx.

Imagina que estás conduciendo un coche. La derivada (o la pendiente de la línea tangente) te dice la dirección exacta en la que te estás moviendo en ese instante. Es la velocidad instantánea de tu cambio de posición.

En resumen, los incrementos (Δx, Δy) representan cambios finitos, mientras que los diferenciales (dx, dy) representan cambios infinitesimalmente pequeños. La relación dy/dx nos da la pendiente de la línea tangente a la curva, lo que nos proporciona información valiosa sobre cómo está cambiando la función en un punto específico.

¡Espero que esto te haya ayudado a comprender la interpretación geométrica de incrementos y diferenciales! ¡Sigue practicando y explorando!