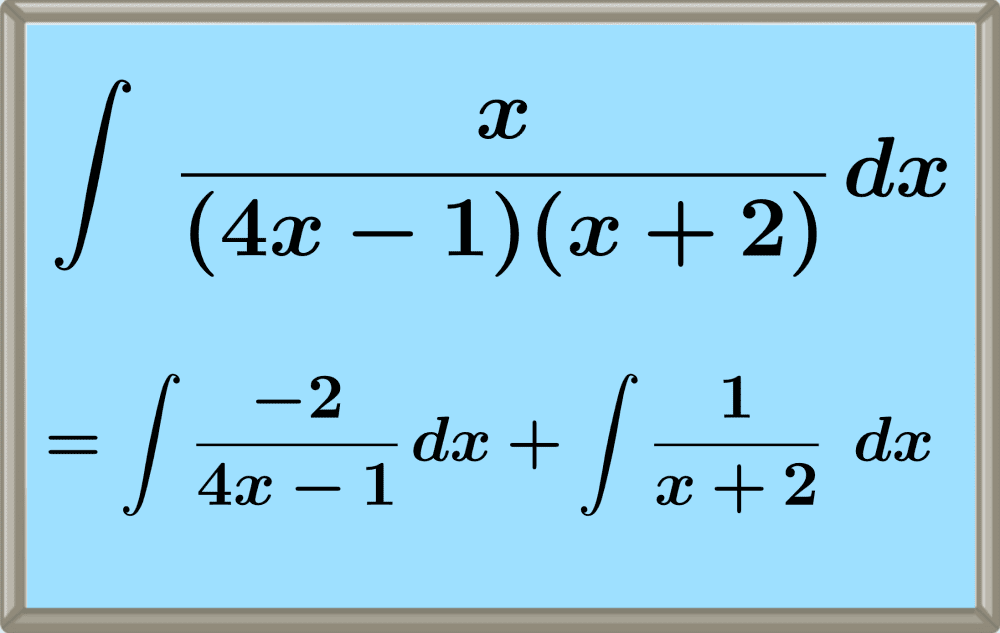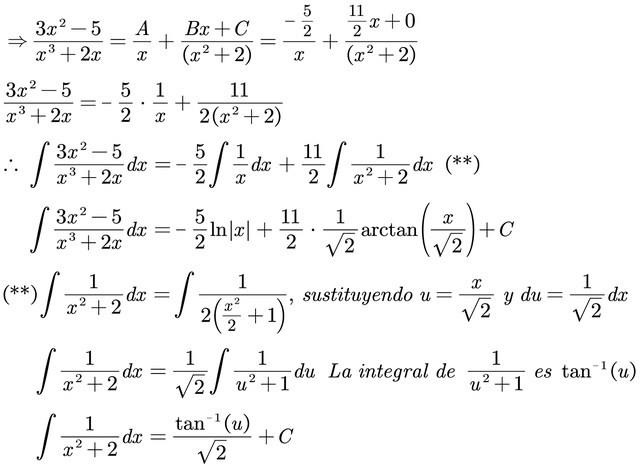Metodo De Integracion De Fracciones Parciales

El método de integración de fracciones parciales es una técnica poderosa. Se usa para integrar funciones racionales.
¿Qué es una Fracción Racional?
Una fracción racional es una expresión de la forma P(x) / Q(x). P(x) y Q(x) son polinomios. Q(x) no puede ser cero.
¿Cuándo Usar Fracciones Parciales?
Se utiliza cuando tenemos una fracción racional. El grado de P(x) debe ser menor que el grado de Q(x). Si no lo es, primero realizamos división larga.
Pasos del Método
Primero, factorizamos el denominador Q(x) completamente. Segundo, expresamos la fracción original como una suma de fracciones más simples. Estas fracciones tienen denominadores que son factores de Q(x).
Tipos de Factores
Existen varios tipos de factores. Cada uno tiene una descomposición diferente. Estos son factores lineales no repetidos, factores lineales repetidos, factores cuadráticos no repetidos y factores cuadráticos repetidos.
Factores Lineales No Repetidos
Si Q(x) tiene un factor (ax + b), no repetido, su descomposición será A / (ax + b). A es una constante a determinar.
Ejemplo: Consideremos la integral de (1 / (x2 - 1)) dx. Factorizamos el denominador: x2 - 1 = (x - 1)(x + 1). Por lo tanto, 1 / (x2 - 1) = A / (x - 1) + B / (x + 1).
Factores Lineales Repetidos
Si Q(x) tiene un factor (ax + b)n, su descomposición será A1 / (ax + b) + A2 / (ax + b)2 + ... + An / (ax + b)n. A1, A2, ..., An son constantes a determinar.
Ejemplo: Consideremos la integral de (1 / (x + 1)2) dx. La descomposición será A / (x + 1) + B / (x + 1)2.
Factores Cuadráticos No Repetidos
Si Q(x) tiene un factor (ax2 + bx + c), donde b2 - 4ac < 0 (es decir, no tiene raíces reales), su descomposición será (Ax + B) / (ax2 + bx + c). A y B son constantes a determinar.
Ejemplo: Consideremos la integral de (x / (x2 + 1)) dx. La descomposición será (Ax + B) / (x2 + 1). En este caso, al ser la derivada del denominador 2x, se resuelve directamente o con una sustitución simple.
Factores Cuadráticos Repetidos
Si Q(x) tiene un factor (ax2 + bx + c)n, donde b2 - 4ac < 0, su descomposición será (A1x + B1) / (ax2 + bx + c) + (A2x + B2) / (ax2 + bx + c)2 + ... + (Anx + Bn) / (ax2 + bx + c)n. Ai y Bi son constantes a determinar.
Determinando las Constantes
Después de establecer la descomposición, multiplicamos ambos lados de la ecuación por Q(x). Esto elimina los denominadores. Luego, igualamos los coeficientes de los términos correspondientes en ambos lados de la ecuación resultante. Esto nos da un sistema de ecuaciones. Resolvemos este sistema para encontrar las constantes A, B, etc.
Integrando las Fracciones Parciales
Una vez que hemos encontrado las constantes, integramos cada fracción parcial individualmente. Las integrales resultantes suelen ser integrales básicas. Incluyen logaritmos, funciones arco tangente o potencias.
Ejemplo: Volviendo al ejemplo de 1 / (x2 - 1) = A / (x - 1) + B / (x + 1). Multiplicando por (x2 - 1), obtenemos 1 = A(x + 1) + B(x - 1). Expandiendo, 1 = (A + B)x + (A - B). Igualando los coeficientes, A + B = 0 y A - B = 1. Resolviendo, A = 1/2 y B = -1/2. Por lo tanto, la integral es (1/2) ln|x - 1| - (1/2) ln|x + 1| + C.
Aplicaciones
Las fracciones parciales tienen aplicaciones en diversas áreas. Incluyen la resolución de ecuaciones diferenciales. También se usan en la transformada de Laplace. Además, se aplican en ingeniería eléctrica y en problemas de flujo de calor.