Metodos De Demostracion En Geometria Ejemplos

En la enseñanza de la geometría, comprender los métodos de demostración es crucial. Es la base para que los estudiantes no solo vean, sino que entiendan por qué las cosas son como son. Esta guía ofrece un enfoque práctico para abordar este tema en el aula, junto con consejos y trucos.

Métodos Comunes de Demostración Geométrica

Existen varios métodos de demostración. Cada uno tiene sus propias fortalezas y aplicaciones. Familiarizarse con ellos es esencial para cualquier estudiante de geometría. Aquí, exploraremos algunos de los más utilizados.

Demostración Directa: Este es el método más sencillo. Se parte de las hipótesis dadas. Luego, mediante una secuencia lógica de pasos, se llega a la conclusión deseada. Cada paso debe estar justificado por un axioma, postulado, definición o teorema previamente demostrado.

Demostración por Contradicción: Aquí, se asume que la conclusión que queremos probar es falsa. A partir de esta suposición, se deducen consecuencias lógicas. Si alguna de estas consecuencias contradice una hipótesis, un axioma o un teorema conocido, entonces la suposición inicial debe ser falsa. Esto implica que la conclusión original es verdadera.

Demostración por Contraposición: Este método se basa en la equivalencia lógica entre una afirmación y su contrapositiva. La contrapositiva de "Si P, entonces Q" es "Si no Q, entonces no P". Para demostrar una afirmación, demostramos su contrapositiva. Si la contrapositiva es verdadera, la afirmación original también lo es.

Demostración por Inducción Matemática: Aunque menos común en geometría básica, es útil para demostrar afirmaciones que se aplican a una secuencia infinita de objetos geométricos. Por ejemplo, el número de regiones en que se divide un círculo al trazar n cuerdas.

Consejos para la Enseñanza

Presentar estos métodos puede ser un desafío. Sin embargo, con el enfoque correcto, se puede hacer más accesible y atractivo para los estudiantes. Estos son algunos consejos para ayudar en la enseñanza:

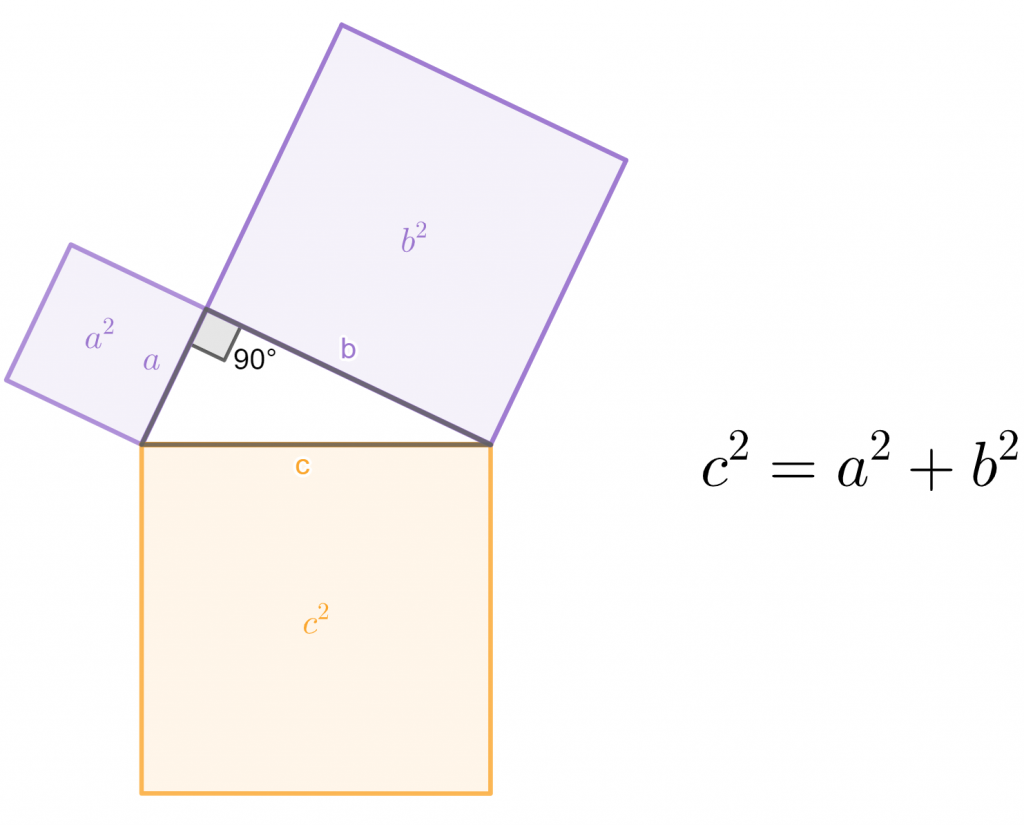
Comenzar con Ejemplos Concretos: En lugar de comenzar con definiciones abstractas, mostrar ejemplos concretos. Un ejemplo sencillo de demostración directa podría ser demostrar que los ángulos opuestos por el vértice son iguales.

Utilizar Diagramas Visuales: La geometría es inherentemente visual. Utilizar diagramas claros y bien etiquetados. Permite a los estudiantes visualizar las relaciones entre los diferentes elementos geométricos. Software de geometría dinámica como GeoGebra puede ser muy útil.

Fomentar la Participación Activa: No solo explicar los métodos. Involucrar a los estudiantes en el proceso de demostración. Pedirles que sugieran el siguiente paso, que justifiquen una afirmación o que identifiquen posibles errores en una demostración propuesta.

Proporcionar Retroalimentación Detallada: Cuando los estudiantes intenten realizar demostraciones, proporcionar retroalimentación detallada. Señalar tanto los aciertos como los errores. Explicar por qué una afirmación es correcta o incorrecta, y cómo se podría mejorar la demostración.

Errores Comunes y Cómo Evitarlos

Los estudiantes a menudo cometen errores comunes al aprender sobre los métodos de demostración. Estar al tanto de estos errores y saber cómo abordarlos puede mejorar significativamente la comprensión de los estudiantes.

Confundir Hipótesis y Conclusión: Los estudiantes pueden tener dificultades para identificar cuál es la hipótesis y cuál es la conclusión de una afirmación. Practicar la identificación de hipótesis y conclusiones en diferentes enunciados geométricos. Ayuda a aclarar esta distinción.

Saltarse Pasos en la Demostración: A veces, los estudiantes se saltan pasos en una demostración. Asumen que ciertas afirmaciones son obvias. Insistir en la importancia de justificar cada paso. Incluso aquellos que parecen evidentes.

Razonamiento Circular: Utilizar la conclusión para justificar un paso en la demostración. Esto es un error lógico grave. Enfatizar la necesidad de que cada paso se base en axiomas, postulados o teoremas previamente demostrados. Nunca en la conclusión que se intenta demostrar.

Hacerlo Atractivo

Para hacer que el tema sea más atractivo, intentar lo siguiente:

Conexiones con el Mundo Real: Mostrar cómo los conceptos geométricos y los métodos de demostración se aplican en el mundo real. Por ejemplo, explicar cómo la geometría se utiliza en la arquitectura, la ingeniería o la navegación.

Juegos y Rompecabezas: Incorporar juegos y rompecabezas geométricos en la enseñanza. Esto puede hacer que el aprendizaje sea más divertido y estimulante. Por ejemplo, el Tangram puede ayudar a desarrollar el razonamiento espacial y la capacidad de resolver problemas geométricos.