Momento De Inercia De Una Barra Con Dos Masas

El momento de inercia es una medida de la resistencia de un objeto a los cambios en su velocidad de rotación. Para una barra rígida con dos masas puntuales unidas a ella, el momento de inercia se calcula sumando las contribuciones de cada masa y la barra (si su masa es significativa).
Cálculo del Momento de Inercia: La fórmula general es I = Σ mr², donde 'I' es el momento de inercia, 'm' es la masa de cada objeto y 'r' es la distancia de cada objeto al eje de rotación. Para nuestra barra con dos masas, si despreciamos la masa de la barra, la fórmula se simplifica considerablemente.
Eje de Rotación: La ubicación del eje de rotación es crucial. Si el eje pasa por el centro de la barra, el cálculo es diferente a si pasa por uno de los extremos o cualquier otro punto. La distancia 'r' en la fórmula siempre se mide desde la masa hasta el eje de rotación.
Despreciando la Masa de la Barra: Si la masa de la barra es mucho menor que las masas puntuales, podemos ignorarla. Entonces, el momento de inercia total es simplemente la suma de los momentos de inercia de las dos masas: I = m₁r₁² + m₂r₂².
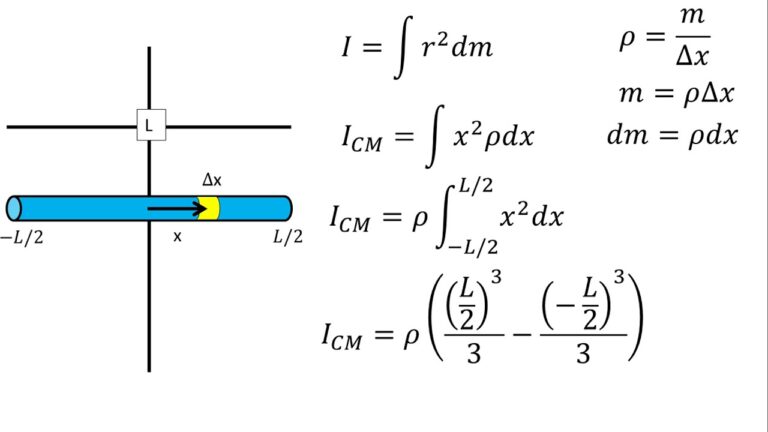
Considerando la Masa de la Barra: Si la masa de la barra es significativa, necesitamos añadir su contribución al momento de inercia total. El momento de inercia de una barra delgada de longitud L y masa M que rota alrededor de un eje perpendicular a la barra que pasa por su centro es (1/12)ML². Si el eje pasa por un extremo, es (1/3)ML².
Ejemplo 1: Una barra de masa despreciable tiene dos masas de 2 kg y 3 kg unidas a sus extremos, que están a 1 metro de distancia. El eje de rotación está en el centro de la barra. Entonces r₁ = 0.5 m y r₂ = 0.5 m. El momento de inercia es I = (2 kg)(0.5 m)² + (3 kg)(0.5 m)² = 1.25 kg·m².
Ejemplo 2: Misma barra con las mismas masas, pero el eje de rotación está en el extremo donde está la masa de 2 kg. Entonces r₁ = 0 m (la masa de 2 kg está en el eje) y r₂ = 1 m. El momento de inercia es I = (2 kg)(0 m)² + (3 kg)(1 m)² = 3 kg·m².
Aplicaciones en el Mundo Real: El momento de inercia es fundamental en el diseño de máquinas rotativas, como motores, turbinas y ruedas. Comprender y calcular el momento de inercia permite optimizar el rendimiento y la estabilidad de estos sistemas, minimizando vibraciones y maximizando la eficiencia energética. También es relevante en el análisis del movimiento de objetos en deportes, como el patinaje artístico o el lanzamiento de martillo.