Proceso De Cálculo Del Método De Análisis De Variaciones

¡Hola! Vamos a explorar el Método de Análisis de Variaciones. Piénsalo como un detective. Buscamos cómo pequeños cambios afectan un sistema. Usaremos un enfoque visual para entenderlo mejor.

Primer Paso: Identificar la Función Principal

Imagínate una receta para un pastel. La cantidad de harina afecta el resultado final. La receta completa es nuestra función principal. Esta función depende de otras variables, como la cantidad de harina, azúcar y huevos. Identificamos esta función para saber qué estamos analizando.

En términos matemáticos, esta función se escribe así: J[y(x)]. Significa que el valor de J depende de la función y(x). Por ejemplo, J puede representar la longitud de una curva, y y(x) la ecuación de esa curva. Queremos encontrar la función y(x) que hace que J sea lo más grande o lo más pequeña posible.

Segundo Paso: Introducir una Variación

Ahora, cambiamos ligeramente uno de los ingredientes del pastel. Añadimos un poco más de harina. Esa pequeña modificación es nuestra variación. Representamos esta variación con la letra griega δ (delta). δy(x) representa un pequeño cambio en la función y(x).

Matemáticamente, reemplazamos y(x) por y(x) + εη(x). Aquí, ε es un número muy pequeño. η(x) es una función arbitraria, que representa la forma de la variación. Piensa en η(x) como la "forma" en que añadimos o quitamos harina. Queremos saber cómo esta variación afecta el pastel.

Tercer Paso: Calcular el Cambio en la Función Principal

Al agregar más harina, el pastel cambia. Puede ser más denso o más seco. Calculamos cómo la función principal (el "pastel") cambia debido a la variación en la cantidad de harina. Esto significa calcular J[y(x) + εη(x)].

Usamos una expansión de Taylor para aproximar este cambio. Es como "desglosar" el cambio en pequeñas partes. Nos enfocamos en el término que es lineal con respecto a ε. Este término nos da una idea de cómo la función J cambia inicialmente con la variación.

Cuarto Paso: Encontrar la Condición de Estacionariedad

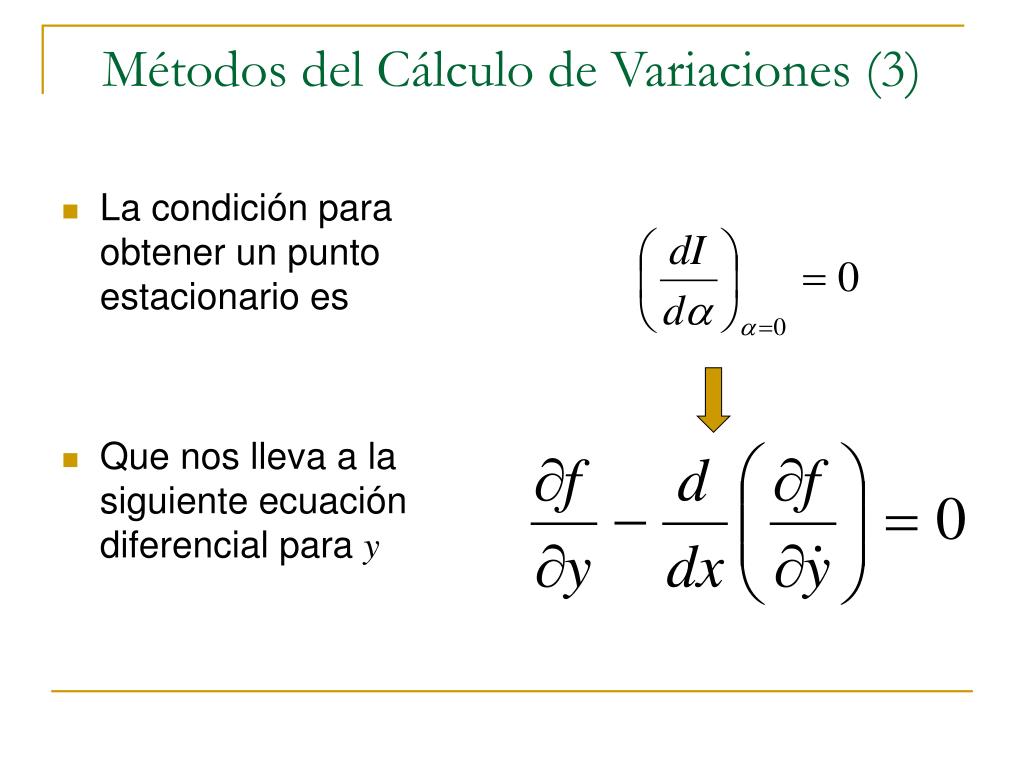
Queremos que el pastel sea lo mejor posible. Esto significa encontrar la cantidad de harina que hace que el pastel sea óptimo. En términos matemáticos, queremos que el cambio en J (debido a la variación) sea cero. Esto se llama la condición de estacionariedad.

Esta condición implica que la integral de cierta expresión, multiplicada por η(x), debe ser cero. Como η(x) es arbitraria, la expresión dentro de la integral debe ser cero. Esta condición nos lleva a una ecuación diferencial conocida como la ecuación de Euler-Lagrange.

Quinto Paso: Resolver la Ecuación de Euler-Lagrange

La ecuación de Euler-Lagrange es nuestra clave. Es una ecuación diferencial que describe la función y(x) que hace que J sea extrema. Resolver esta ecuación nos da la función óptima.

Resolver la ecuación de Euler-Lagrange puede ser complicado. Depende de la forma específica de la función J. A veces, necesitamos usar técnicas de integración especiales. En otros casos, la solución puede ser una función conocida, como una línea recta o una curva parabólica.

Ejemplo Práctico: La Curva Más Corta

Imagina que quieres ir de un punto A a un punto B. ¿Cuál es la ruta más corta? Una línea recta, ¿verdad? Podemos usar el Análisis de Variaciones para demostrarlo.

En este caso, J representa la longitud de la curva que conecta los puntos A y B. y(x) es la ecuación de la curva. Aplicando los pasos anteriores, llegaremos a la conclusión de que la ecuación de Euler-Lagrange describe una línea recta. ¡Confirmado!

El Método de Análisis de Variaciones es una herramienta poderosa. Nos ayuda a encontrar funciones que optimizan ciertas cantidades. Requiere práctica y paciencia. Pero con esta guía visual, espero que te resulte más accesible. ¡Sigue practicando y dominarás este método!