Tipos De Funciones Matematicas Y Sus Graficas

Las funciones matemáticas son relaciones entre un conjunto de entradas (el dominio) y un conjunto de salidas (el rango). Para cada entrada, la función produce exactamente una salida. Su representación gráfica en un plano cartesiano es una herramienta fundamental para comprender su comportamiento.
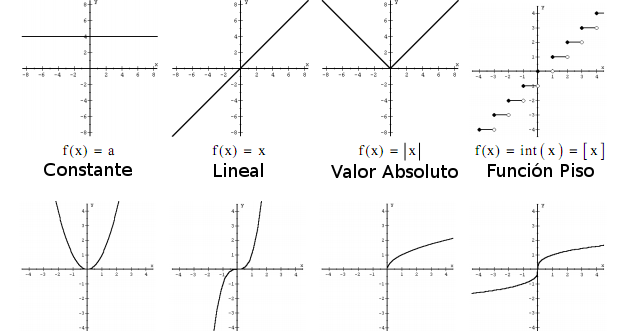
Existen varios tipos de funciones, cada uno con características distintivas. A continuación, exploraremos algunos de los más comunes:
Función Lineal: Su ecuación general es f(x) = mx + b, donde m es la pendiente y b es la intersección con el eje y. La gráfica es una línea recta. Un ejemplo simple es f(x) = 2x + 1.
Función Cuadrática: Se define como f(x) = ax2 + bx + c, donde a, b y c son constantes, y a ≠ 0. La gráfica es una parábola. El vértice de la parábola representa el máximo o mínimo de la función. Un ejemplo es f(x) = x2 - 4x + 3.
Función Exponencial: Tiene la forma f(x) = ax, donde a es una constante positiva diferente de 1. La gráfica muestra un crecimiento o decrecimiento rápido. Un ejemplo es f(x) = 2x.
Función Logarítmica: Es la inversa de la función exponencial. Se escribe como f(x) = loga(x), donde a es la base del logaritmo. La gráfica muestra un crecimiento lento para valores grandes de x. Un ejemplo es f(x) = log2(x).
Función Trigonométrica: Incluye funciones como seno (sin(x)), coseno (cos(x)) y tangente (tan(x)). Son funciones periódicas, lo que significa que sus valores se repiten en intervalos regulares. Las gráficas muestran ondas.
Función Polinómica: Es una función que involucra solo potencias enteras no negativas de la variable x. Un ejemplo es f(x) = x3 + 2x2 - x + 5. El grado del polinomio determina la forma general de la gráfica.
La comprensión de las gráficas de funciones es crucial para analizar su comportamiento. La pendiente de la tangente a la curva en un punto da la tasa de cambio instantánea. Las intersecciones con los ejes x e y revelan información importante sobre los valores de la función.
Las funciones matemáticas tienen aplicaciones en diversas áreas. Por ejemplo, la función lineal se utiliza en economía para modelar relaciones entre oferta y demanda, mientras que la función exponencial se aplica en biología para modelar el crecimiento de poblaciones. La física usa las funciones trigonométricas para describir fenómenos ondulatorios.