Cuál De Las Siguientes Funciones Es Creciente

Entender qué significa que una función sea *creciente* es fundamental en matemáticas. Nos permite analizar cómo cambia el valor de una función a medida que su entrada varía. En este artículo, exploraremos este concepto en detalle.

¿Qué es una Función Creciente?

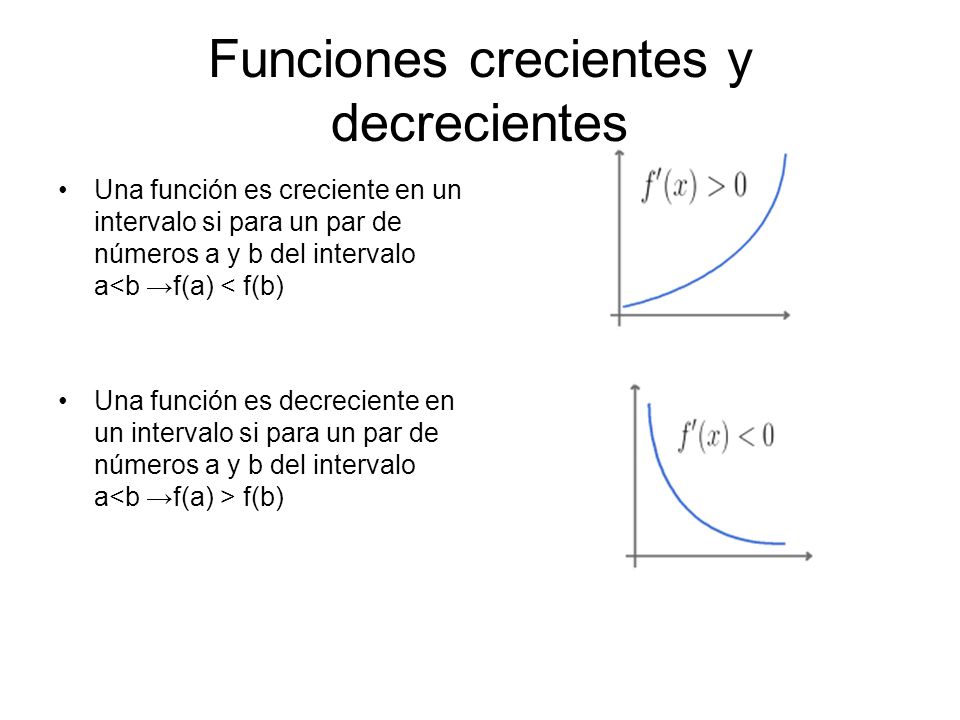
Una función es *creciente* en un intervalo si, al aumentar el valor de la variable independiente (generalmente *x*), el valor de la función (generalmente *f(x)* o *y*) también aumenta. En términos más formales:

Si tenemos dos puntos, *x₁* y *x₂*, en un intervalo, y *x₁* < *x₂*, entonces *f(x₁)* < *f(x₂)*. Esto significa que, a medida que nos movemos hacia la derecha en el eje *x*, la gráfica de la función se eleva.

Ejemplos de Funciones Crecientes

Veamos algunos ejemplos comunes para ilustrar este concepto:

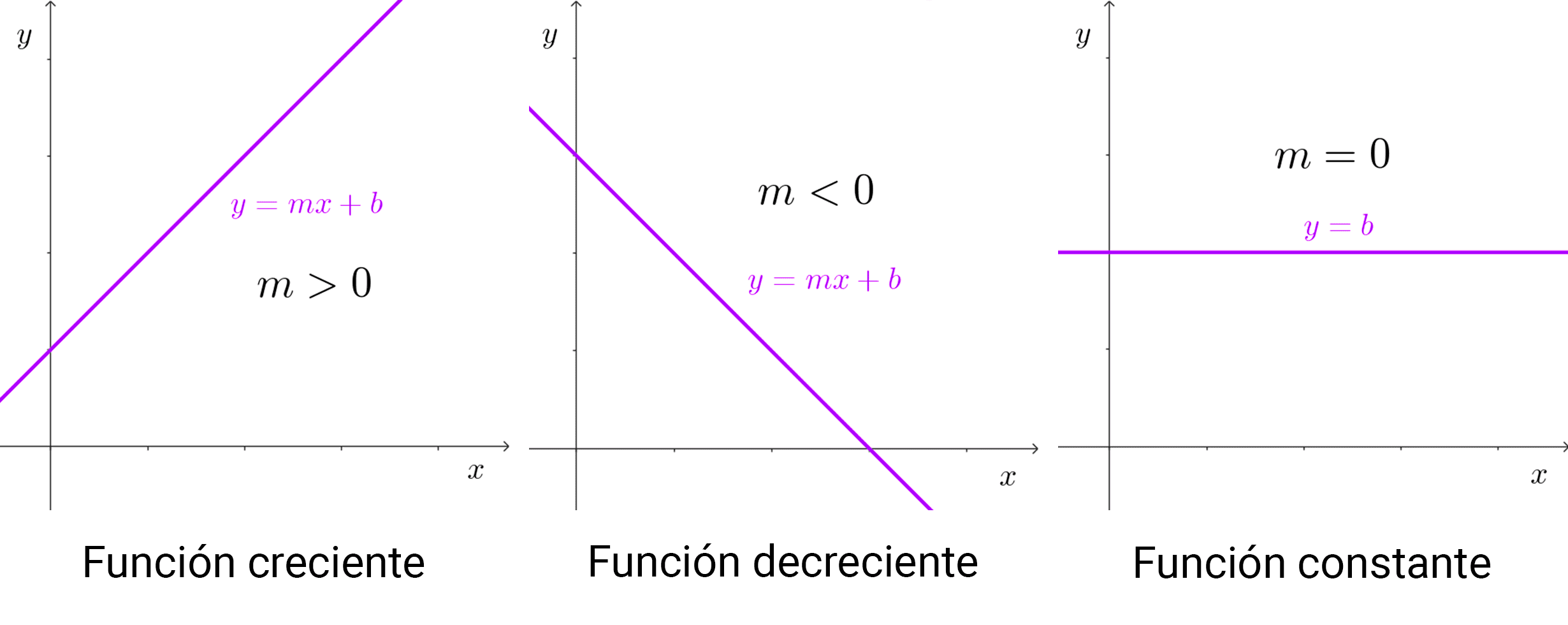
Función Lineal con Pendiente Positiva: Consideremos la función *f(x) = 2x + 1*. A medida que *x* aumenta, *f(x)* también aumenta. Por ejemplo, si *x = 1*, entonces *f(1) = 3*. Si *x = 2*, entonces *f(2) = 5*. Esta es una función creciente en todo su dominio.

Función Exponencial con Base Mayor que 1: La función *f(x) = 3ˣ* es otro ejemplo. Si *x = 0*, *f(0) = 1*. Si *x = 1*, *f(1) = 3*. Si *x = 2*, *f(2) = 9*. Claramente, a medida que *x* aumenta, *f(x)* también aumenta exponencialmente. Siempre que la base de la función exponencial sea mayor que 1, la función será creciente.

Cómo Determinar si una Función es Creciente

Existen varias maneras de determinar si una función es creciente:

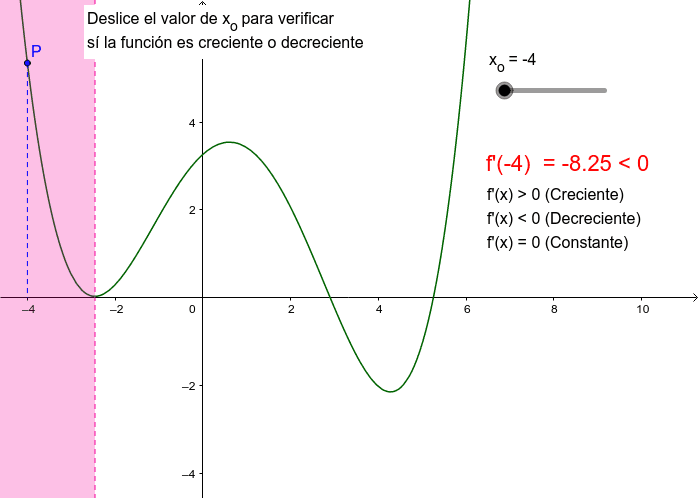
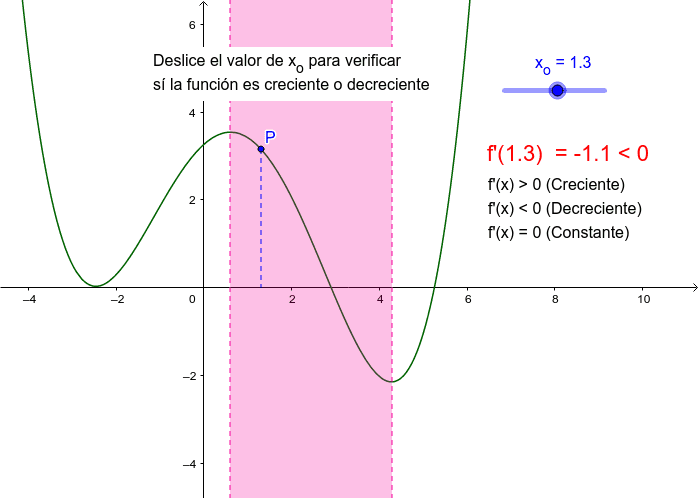
Análisis de la Derivada: En cálculo, la *derivada* de una función nos indica su tasa de cambio. Si la derivada de una función, *f'(x)*, es positiva en un intervalo, entonces la función es creciente en ese intervalo. Si *f'(x) > 0*, entonces *f(x)* es creciente.

Análisis Gráfico: Podemos observar la gráfica de la función. Si la gráfica "sube" de izquierda a derecha, entonces la función es creciente. Presta atención a los intervalos específicos. Una función puede ser creciente en un intervalo y decreciente en otro.

Tabla de Valores: Podemos crear una tabla de valores para diferentes valores de *x* y observar cómo cambia *f(x)*. Si *f(x)* siempre aumenta a medida que *x* aumenta, entonces la función es creciente.

Funciones Decrecientes y Constantes

Es importante mencionar las funciones *decrecientes* y *constantes* para contrastar con las funciones crecientes.

Una función es *decreciente* si el valor de la función disminuye a medida que el valor de la variable independiente aumenta. En este caso, si *x₁* < *x₂*, entonces *f(x₁)* > *f(x₂)*.

Una función es *constante* si el valor de la función permanece igual a medida que el valor de la variable independiente cambia. En este caso, *f(x) = c*, donde *c* es una constante.

Aplicaciones Prácticas

El concepto de funciones crecientes es fundamental en muchas áreas, incluyendo:

Economía: La ley de la oferta y la demanda puede modelarse con funciones. La oferta generalmente es una función creciente del precio.

Física: La velocidad de un objeto que acelera constantemente puede representarse mediante una función creciente del tiempo.

Informática: El tiempo de ejecución de algunos algoritmos puede aumentar a medida que aumenta el tamaño de la entrada. Analizar si esta función es creciente ayuda a entender la eficiencia del algoritmo.

En resumen, comprender las funciones crecientes es esencial para analizar y modelar fenómenos del mundo real en diversas disciplinas. Al reconocer las características y propiedades de las funciones crecientes, podemos obtener una mejor comprensión de los patrones y tendencias que nos rodean.