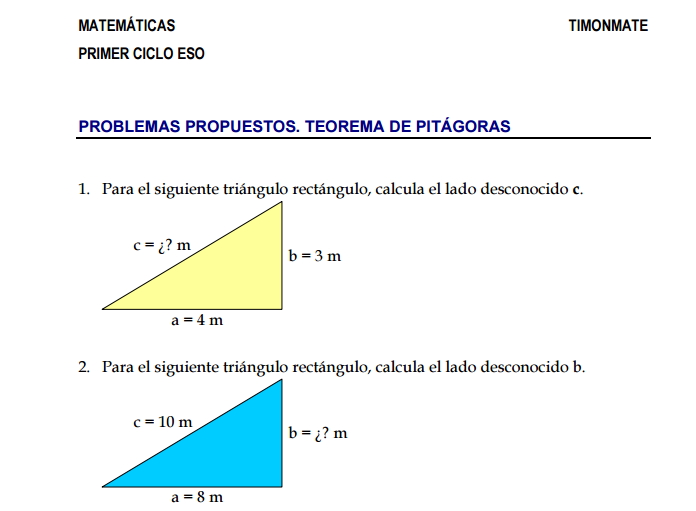
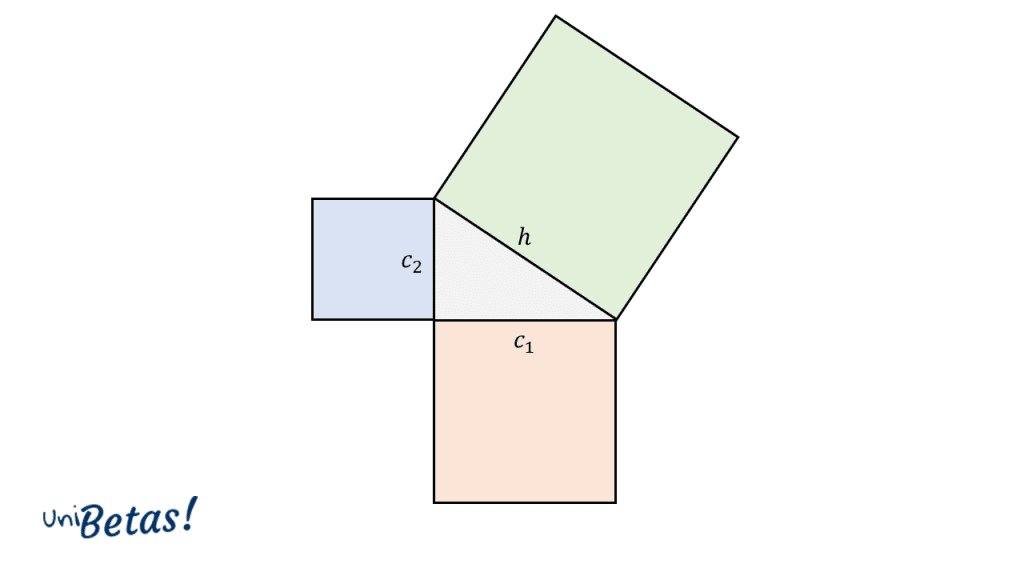
Ejemplos De Problemas De Teorema De Pitagoras

El Teorema de Pitágoras es una de las ideas más fundamentales en geometría. En esencia, define la relación entre los lados de un triángulo rectángulo. Un triángulo rectángulo es aquel que tiene un ángulo de 90 grados, también llamado ángulo recto.
La definición clave: en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados (llamados catetos). Matemáticamente, esto se escribe como: a2 + b2 = c2, donde 'c' es la hipotenusa, y 'a' y 'b' son los catetos.
Ejemplo 1: Imagina un triángulo rectángulo donde un cateto (a) mide 3 cm y el otro cateto (b) mide 4 cm. Para encontrar la hipotenusa (c), aplicamos el teorema: 32 + 42 = c2, lo que significa 9 + 16 = c2, entonces 25 = c2. Por lo tanto, c = √25 = 5 cm. La hipotenusa mide 5 cm.
Ejemplo 2: Ahora, supongamos que conocemos la hipotenusa (c = 13 cm) y un cateto (a = 5 cm). Queremos encontrar el otro cateto (b). Usamos la fórmula: 52 + b2 = 132, lo que significa 25 + b2 = 169, entonces b2 = 169 - 25 = 144. Por lo tanto, b = √144 = 12 cm.
El Teorema de Pitágoras tiene aplicaciones prácticas en la vida cotidiana. Por ejemplo, se usa en construcción para asegurar que las esquinas sean perfectamente cuadradas. También se utiliza en navegación para calcular distancias, y en diseño gráfico para crear imágenes precisas. Imagina que estás construyendo una rampa para discapacitados; necesitas saber la longitud de la rampa (la hipotenusa) basándote en la altura (un cateto) y la distancia horizontal (el otro cateto). ¡El Teorema de Pitágoras es la herramienta perfecta para ese trabajo!