Encontrar Los Ceros De Una Funcion Polinomial

¡Hola a todos! ¡Prepárense para dominar la búsqueda de los ceros de una función polinomial! Vamos a repasar las herramientas y técnicas que necesitarán para tener éxito en su examen.
¿Qué son los Ceros de una Función Polinomial?
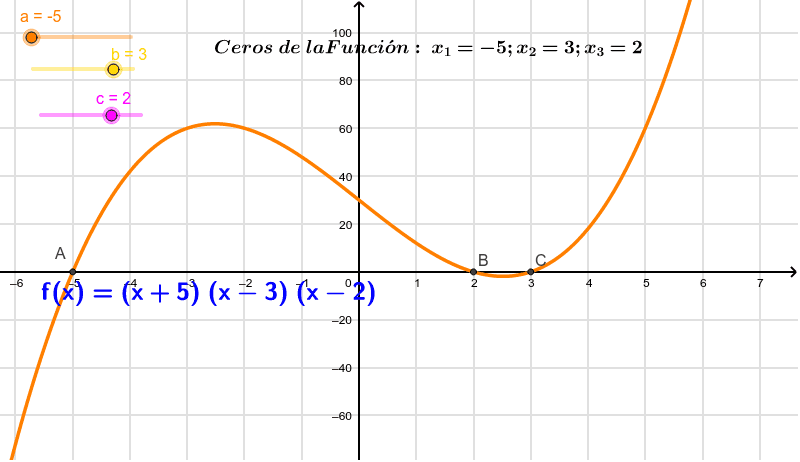
Un cero, también llamado raíz o solución, de una función polinomial f(x) es un valor de x que hace que f(x) = 0. En otras palabras, son los puntos donde la gráfica de la función cruza o toca el eje x. Imaginen que están buscando los lugares secretos donde la función se esconde en el eje x.
Entender esto es crucial. Los ceros nos dan información valiosa sobre el comportamiento de la función. Nos ayudan a graficarla y a resolver ecuaciones.
Herramientas Esenciales
Aquí están las herramientas clave que necesitarán. Dominar estas técnicas les asegurará un buen desempeño. Practiquen con cada una de ellas.
1. Factorización
La factorización es expresar el polinomio como un producto de factores más simples. Si pueden factorizar el polinomio, encontrar los ceros es pan comido. Cada factor igualado a cero les dará un cero de la función.
Por ejemplo, si tienen f(x) = x2 - 4, pueden factorizarlo como (x + 2)(x - 2). Igualando cada factor a cero: x + 2 = 0 da x = -2 y x - 2 = 0 da x = 2. ¡Así que los ceros son -2 y 2!
2. Teorema del Factor y del Residuo
El Teorema del Factor dice que si f(c) = 0, entonces (x - c) es un factor de f(x). El Teorema del Residuo nos ayuda a encontrar el residuo al dividir un polinomio por (x - c), que es igual a f(c). ¡Estos teoremas son detectives que nos ayudan a encontrar factores!
Usen la división sintética para probar posibles ceros. Si el residuo es cero, ¡encontraron un factor!
3. Teorema de las Raíces Racionales
El Teorema de las Raíces Racionales les da una lista de posibles ceros racionales. La lista se construye dividiendo los factores del término constante (el número sin x) por los factores del coeficiente principal (el número que multiplica la x con la potencia más alta).
Por ejemplo, si tienen f(x) = 2x3 + x2 - 7x - 6, las posibles raíces racionales son ±1, ±2, ±3, ±6, ±1/2, ±3/2. ¡Luego, prueben estos valores usando división sintética!
4. Fórmula Cuadrática
Para polinomios de grado 2 (cuadráticos), la fórmula cuadrática es su mejor amiga. La fórmula es: x = (-b ± √(b2 - 4ac)) / 2a para la ecuación ax2 + bx + c = 0.
¡Recuerden la fórmula cuadrática! Les salvará la vida en muchos problemas.
Consejos para el Examen
Practiquen, practiquen, practiquen. Cuanto más practiquen, más cómodos se sentirán con estas técnicas. Empiecen con problemas sencillos y avancen a problemas más complejos.
Verifiquen sus respuestas. Sustituyan los ceros que encuentren de nuevo en la función original para asegurarse de que realmente hacen que la función sea igual a cero.
No se rindan. Si un problema les resulta difícil, inténtenlo de nuevo más tarde con una nueva perspectiva. ¡Todos cometemos errores, lo importante es aprender de ellos!
Resumen
Para encontrar los ceros de una función polinomial, recuerden:
- Factorización: Expresar el polinomio como un producto de factores.
- Teorema del Factor y del Residuo: Usar la división sintética para encontrar factores.
- Teorema de las Raíces Racionales: Crear una lista de posibles ceros racionales.
- Fórmula Cuadrática: Resolver ecuaciones cuadráticas.
¡Confío en que están listos para triunfar! ¡Mucho éxito en su examen! ¡Ustedes pueden!